Имитационное моделирование производственных Систем
Одной из основных форм анализа качества, надежности и эффективности производственных систем является имитационное исследование, проводимое на имитационных моделях. Наибольшее распространение в практике исследования качества и эффективности получили цифровые имитационные модели, т. е. модели, реализуемые на цифровых ЭВМ.
При имитационном моделировании алгоритмическая модель системы воспроизводит процесс функционирования системы во времени. При этом имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени. Это позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, что дает возможность оценить характеристики надежности и производительности системы.
Метод имитационного моделирования позволяет решать задачи анализа систем, включая задачи оценки вариантов структуры системы, эффективности различных алгоритмов управления системой, влияния изменения различных параметров системы. Имитационное моделирование может быть использовано для параметрического и структурного синтеза систем.
Имитационное моделирование на ЭВМ имеет достоинства и недостатки. К достоинствам метода имитационного моделирования при исследовании систем можно отнести следующие: имитационная модель позволяет исследовать особенности процесса функционирования системы с учетом любых условий; существенно сократить продолжительность исследования системы по сравнению с натурным экспериментом: включать в план испытаний результаты натурных испытаний реальной системы; варьировать структуру, алгоритмы расчетов и параметры системы, выбрать оптимальный вариант системы.
Основным недостатком имитационного моделирования является то, что решение, полученное с помощью имитационной модели, носит частный характер. Поэтому для полного анализа процесса функционирования системы необходимо многократно воспроизводить имитационный эксперимент, варьируя исходные данные, что увеличивает затраты машинного времени.
В данном разделе рассматриваются принципы построения цифровой имитационной модели процесса функционирования производственной системы с учетом действия различных факторов.
В имитационных моделях имитируется поведение исследуемой системы в некотором интервале времени. Характерными особенностями данных моделей являются порядок изменения временной координаты и способ согласования различных событий в системе. Эти два аспекта имитационных моделей известны как механизм системного времени, обеспечивающий синхронизацию событий и процессов.
Существуют два основных вида механизма системного времени — задание времени при помощи постоянных и с помощью переменных интервалов времени (шагов). Второй механизм известен как моделирование по особым состояниям.
По методу постоянного шага отсчет системного времени ведется через фиксированные, заранее выбранные исследователем интервалы времени. События в модели считаются наступившими в момент окончания этого интервала.
При моделировании по особым состояниям системное время каж дый раз изменяется на величину, строго соответствующую интервалу времени до момента наступления очередного события. Б этом случае события обрабатываются поочередно, в порядке их наступления, и регистрируются как одновременные лишь в том случае, если они одновременны в действительности.
Метод моделирования по особым состояниям сложнее в реализации, чем моделирование с постоянным шагом, так как для него тре буется введение специальной процедуры (календаря событий) для определения момента появления последующих событий и ранжирования их в порядке возрастания.
Метод фиксированных шагов предпочтительнее, если события появляются регулярно, их распределение во времени достаточно равномерно. число событий велико, а продолжительность отдельного события мала.
Метод моделирования но особым состояниям целесообразно использовать, если события распределяются во времени неравномерно или их продолжительность велика. Этот метод позволяет экономить машинное время при моделировании статических систем или систем периодического действия, в которых события могут длительное время не наступать.
В зависимости от способа взаимодействия пользователя с моделью имитационные модели делятся на автоматические и диалоговые. Автоматическими называются имитационные модели, взаимодействие пользователя с которыми сводится только к вводу исходной информации и управлению началом и окончанием работы моделей. Имитационные модели и системы, позволяющие пользователю активно управлять ходом моделирования, называются диалоговыми.
Описанные ниже основные принципы составления алгоритмов статистического имитационного моделирования функционирования ав томатизированных производственных систем предназначены для решения конкретных задач, используемых для исследования технических систем, какими являются печатно-отделочные и брошюровоч — но-переплетные линии.
Автоматизированные линии, используемые в полиграфическом и упаковочном производстве, — это многофазные технические системы с многоканальными комплексами или участками, между которыми устанавливаются транзитные или тупиковые накопители полуфабрикатов. Многоканальные участки могут представлять систему из нескольких параллельно работающих машин и машин, находящихся в холодном резерве. ПС могут обслуживаться операторами, роботами и наладчиками.
Состояние данной системы определяется дискретными состояниями всех входящих в нее элементов. Функционирование подобной системы есть процесс изменения ее состояний под влиянием некоторых потоков событии. Для ПС такими потоками являются потоки отказов и восстановлений элементов системы (машин, накопителей, наладочных устройств, операторов, роботов, наладчиков и др.); заполнения и опустошения накопителей; заявок на проведение работ (но обслуживанию, подготовке рабочего места, профилактическому ремонту и техническому обслуживанию, контролю за качеством продукции, информационному и материальному обслуживанию и т п.); выполнения указанных работ; заявок и проведения регламентированных простоев и др. Перечисленные потоки событий, происходящие по различным причинам (факторам), могут быть разделены на элементарные по видам факторов. Так, потоки отказов и восстановлений элементов могут быть разделены на элементарные потоки по видам отказов; материальные, энергетические и информационные потоки — по видам материалов, полуфабрикатов, сырья, энергии, информации; потоки заявок и выполнения технического обслуживания (ТО) и профилактического ремонта — по видам ТО и ремонта.
Время пребывания элементов системы в состоянии работы или эксплуатации до смены состояния на противоположное, т е. до простоя по V-му фактору, f определяется законом распределения F(t^J, А в состоянии простоя t — законом распределения G(t ) Указанные законы могут быть произвольными распределениями. По функциям распределений формируются реализации случайных времен t и t.
Одним из первых этапов имитационного моделирования fic является анализ состояний их элементов, который заключается в определении вида состояния.
Каждое состояние работоспособности или эксплуатации K—Vo элемента е-го вида по г>-му фактору в Е-ю реализацию процесса функционирования описывается дискретной единичной функцией состояния работоспособност и или эксплуатации вида
1, если k-й элемент находится в рабо тоспособном состоянии или состоянии экспортации до п ростоя по f-му фактору;
2С I = 4
О, если k й элемент находится в состоянии простоя по t> му фактору,
|
A fpk |
|
$vek ~ |
Где е— вид элемента, е = мш, нк, ну, оп, нл, рб; мш — машина; нк — накопитель; ну — наладочное устройство; оп — оператор; нл — наладчик; рб — робот; у— вид фактора (причины простоя), V = в, н, то, пр, пм, и, м, рп, ov хр, оо, ов, кк; в — восстановление: н — наладка; то — техническое обслуживание; пр — профилактические ремонты; пм — подготовка рабочего места; и — информационный простой; м — материальный простой; рп — регламен’тированный перерыв; о — обслуживание; хр — нахождение в холодном резерве; оо — ож идание обслуж и- вания; ов — ожидание восстановления; кк — контроль качества; к— номер элемента в системе, k= k(e), к(м) = Hy Ынк) = Hi; K(on) = Hv А(нл) = ft;
Мрб) = htO, j = lJmfa’1 I=l, nh; D — 1, kon hi; b = 6-1, qft-,
Nh — количество участков Л-й ветви; h = 1, Н — количество параллельно ус гановленных машин на Ьш участке; J л — количество на лвд — чиков, обслуживающих систему; Н— количество ветвей в ПС
Состояние занятости р-хъ рабочего (оператора, наладчика и др.) или робота выполнением V-й работы описывается функцией
1, если оператор (робот) не занят V-и работой; О, если оператор (робот) занят V-й рабо той.
Кроме указанных функций состояний для описания скачков из одного состояния в другое состояние (смены состояния) по т^му фактору предлагается дискретная функция скачка состояния Bvek, имеющая вид
1, если имеет место смена состояния; О, если элемент пребывает в прежнем состоянии.
Связь между потоками событий по определенным факторам ус — танэвливается с помощью коэффициента прерывания или влияния У, образующих матрицу коэффициентов прерывания (влияния), элементы которой имеют значения 1 или 0 в зависимости от фактора прерывания действия определенного потока событий по причине вступления в действие другого фактора. Коэффициент прерывания имеет вид
1, если z фактор Im-ru элемента прерывает действие г;-го фактора для ек-го элемента; О, если прерывания нет
Функции работоспособности или эксплуатации X принимают новые значения скачкообразно, когда некоторое воздействие принимает пороговое значение. Б качестве таких воздействий, ведущих к изменению состояния элементов системы, используются остаточные ресурсы наработки и^и времени эксплуатации до смены состояния элемента на противоположное г^ у остаточные ресурсы времени до окончания простоя по тли причине f^, при достижении нулевого значения которых элементы переходят скачком в противоположное состояние. В зависимости от значений V^ и f ^ функции состояний А могут иметь следующие значения:
1, если г ^ > 0 a frtk = 0 , О, если rvfk = 0 л Fvtk > 0 .
Функция скачка состояния В к зависит также от значений r^wf^w определяется как
1, если
Если/,^ > О,
Где и{ г ), v(j +) — асимметричные единичные функции.
Функции занятости к~ м рабочим или роботом р~го вида выполнением V й работы принимают свои значения при следующих условиях-
АеслиЭЛ*^);
0, если 3(1)[к = Klfd), (6-3°)
К^, = min{к | Хв„ = 1 а .V = 1 л X. w — 0),
Где к — номер рабочего (робота), занятого выполнением V й работы на /~м объекте е-го вида; К^— инициализированный номер K—Ro рабочего (робота), занятого обслуживанием или восстановлением /-го объекта е i о вида, р =■ он, нл; V = в, о, кк; е = мш, нк.
|
^С* — |
|
1, еслнг^О; О, если р. > О, U{}**] |
|
) = |
Как видно из выраженш.’ (6.3U), k-й рабочий (робо г) занимается выполнением тли работы на 1~м объекте [А л =0), если /-й объект тре
бует данной V й работы (Л Р,=0), а / — й рабочий (робот) работоспособен (Х^ = 1) и свободен откакои-либо работы При указанных условиях к~й рабочим (робот) инициализируется под номером К, т е. закрепляется за I м объектом.
|
V Fel |
Функция ожидания 1м объектом е~го вида обслуживания ъто вида рабочим (роботом) р-н специальности определяется как
1, есш Хы = v А, м =0k = К
|
V Хрмш hi] |
О, если Xvd = 0 л тЫщ = 0 v * = 0).
V = о, в, кк; р= оп, нл, рб; к — ЫЩ 0, Функция пребывания у-й машины г то участка /г й ветви в холодном резерве зависит о т функции работоспособности машины и количества машин на участке, занятых работой. Ее определяем по формуле
1, если XBM)IIhij=0v<Хн, ф1 Apr = 1 л
Mhi К =1; кг J
J"hi
0, если XIIMIllAl> —1a X ~~hik)^mhi-m hi,
K=1; k* j
Где M J(— количество резервных машин на Hi—М участке.
Снятие элемента с ожидания и установка его на обслуживание или ремонт проводятся на основании очередности.
Алгоритм формирования очереди зависит от концепции очередности. Снятие с очереди проводится в соответствии 1) с местом элемента в структуре ПС; 2) со значением времени работ или затрат на них; Я) с временем поступления заявки на проведение работ; 4) путем случайного выбора из числа очередников
При зависимости параметров потока но г*-му фактору от производительности элементов ПС в качестве остаточного ресурса наработки принимаем остаточное количество продукции, которое элемент отработает до момента простоя по V-й причине, или остаточное ко личество циклов работы машины. Подобный подсчет полного и остаточного ресурсов наработки приводит к автоматическому учету наложенных простоев, вызванных различными факторами и просто ями других машин и участ ков. Отпадает необходимость в разрабо гке и использовании специального аппарата оценки наложенных просто
ев, что позволяет упростить имитационную модель процесса функционирования ПС.
При независимости параметров потока по v-му фактору от производительности элементов ПС в качестве остаточного ресурса принимаем остаточное время г, которое элемент должен отработать до момента простоя но f-му фактору
Остаточный ресурс наработки его элемента по v-му фактор)’ определяем в виде
Где Кф]ufk — перспективная суммарная наработка к-rо элемента его вида до очередного простоя по т’-му фактору; SR^ti к — фактическая суммарная наработка f-ro элемента по тлму фактору к Е-й реализации процесса функционирования.
^QMA = ^Qyek + ^pvekQmek ‘
Где — номинальная производительность элемента или системы в зависимости от рассматриваемого т>го фактора. Так, Qiviti — Q{vtky если V = в, о, кк; Q^ fk = (7 , если V = п; Q^ — номинальная производительность системы; t — очередная реализация времени работы или эксплуатации элемента или системы до простоя по т>му фактору.
|
^Р vek |
Lvek — + ^pt/A ‘
Ar(F(tpvfk)), Если Bvfk = 1 ЛХггек = 1; О, Если Bvek = 0 v (Bvtk = 1 Л Xlvk = 0),
Где Ar{F(t Ifk)) — оператор алгоритмического типа, определяющий правило получения реализаций случайных величин времени tp ^ по заданным законам их распределения F(t представляющий генератор случайных чисел.
Остаточный ресурс времени простоя элемента по гкму фактору имеет вид
J vek 1 irk oi vek >
Где Fvfk — перспективное суммарное время простоя элемента но и-му фактору; S1 ^ — текущее (фактическое) суммарное время простоя элемента по тлму фактору.
1 vek 1 «А ^ Lvk ‘
Где tbA — реализация очередного времени простоя по г>му фактору.
MG(tvek)), если Bmk = 1AXvek =0; 0, если Bvek =0v(Bvek = 1 л Xvek =1),
Где Ar(G{^)) — оператор алгоритмического типа, определяющий правило получения реализаций случайных величин времени ^по заданному закону их распределения или генератор случайных чисел t^.
|
^vek ~ |
|
<7 > |
|
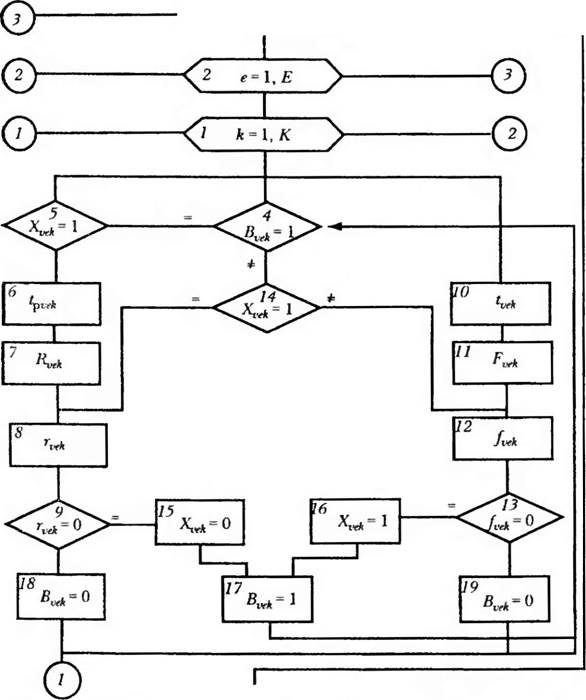
Рас. 6.3, Фрагмент алгоритма оценки функций состояний X‘ и скачков В Элементов ПС |
|
W* |
Последовательность оценки X и Jэлементов по факторам представлена на приведенном ниже фрагменте алгоритма (рис. 6.3).
Алгоритмическая модель анализа функций состояний и скачков состояний элементов работает следующим образом.
Анализ состояния всех элементов по каждому фактору проводится последовательно от элемента к элемент)’ в порядке их следования в структурной схеме системы. Положим, например, что проводится анализ состояния элементов системы при действии фактора потоков отказов и восстановлений элементов. В блоке задания начальных условий содержатся исходные значения функций состояний и скачков всех элементов: X ^ = 1 и В! = 1. Это означает, что все элементы в момент T = О работоспособны (Х^ = 1) и вступают в работу (имеет место скачок состояний элементов) (В =1).
В блоках 4 и б проводится сравнение значений функций состояний и скачков с помощью условных операторов. Если Х^ = 1 и = 1, то в блоке 6с помощью генератора случайных чисел вырабатывается реализация времени работы элемента до очередного его отказа ^ В блоке 7 рассчитывается перспективная наработка (в экземплярах продукции или циклах) R до очередного отказа. Далее в блоке 8 Определяется остаточный ресурс наработки до отказа элемента г^. В блоке сравнения 9 проверяется наличие остаточного ресурса. Если остаточный ресурс не равен нулю (больше нуля) (г^ >0), то функции состояния элемента Х^к присваивается значение 1 (Х^ = 1), а функции скачка В — значение 0 0), т. е. элемент продолжает быть работоспособным, скачок (переход) в новое состояние (состояние восстановления) отсутствует, наблюдается переход к анализу состояния следующего элемента с помощью оператора цикла 3 или переход к анализу элементов другого вида с помощью оператора цикла 2.
При г^=0 элемент переводится в состояние отказа и восстановления, функции состояния Х^ элемента присваивается значение 0 (Х^ = 0), а функции скачка В k элемента — значение 1 (В^ =1). После этого управление процедурой анализа передается блокам сравнения 4 и 5.
Так как имеет место скачок состояния элемента (из состояния работы в состояние отказа и восстановления) (/f = 1) и элемент не работоспособен (Х^ = 0), то после блока сравнения 5 в блоке 10С помощью генератора случайных чисел вырабатывается реализация времени восстановления t ^. Далее в блоке 11 определяется перспективное суммарное время восстановления F элемента, а в блоке 12 рассчитывается остаточный ресурс восстановления до конца ремонта и начала работы. В блоке 13 оператор сравнения проверяет наличие остаточного ресурса восстановления> 0). Если это так, то элемент остается в состоянии восстановления, а функции скачка BvA элемента присваивается значение 0 в блоке 19 (В= 0), осуществляется переход к анализу состояния следующего элемента с блока 3 или элементов другого вида с блока 2.
При исчерпании ресурса восстановления (восстановление элемента закончилось) (J = 0) в блоке 16 элемент переводится в состояние работы (Х^ = 1), а функции скачка Btvi присваивается значение 1 1), управление процедурой анализа передается далее блоку 4.
Если в ходе функционирования системы скачка состояния нет (В ^ = 0), а элемент продолжает быть работоспособным (Х л = 1) или быть в состоянии восстановления (Х^ = 0), то после блоков сравнений 4 и /’/следует расчет остаточного ресурса работы г^ при ХгЛ = 1 или остаточного ресурса восстановления f при Хл = 0. При смене фактора анализ продолжается с блока 1.
Описанные функции состояний используются для дальнейшей оценки параметров процесса функционирования IIC.
Параметрами процесса функционирования ПС являются времена состояний элементов и системы, текущие производительности элементов ПС, ее участков и системы в целом, текущие суммарные наработки и времена простоев элементов и системы, текущие уровни запасов полуфабрикатов в накопителях, фактический коэффициент использования и производительность системы.
Каждое состояние элемента характеризуется временем состояния Д^ а если спроецировать все моменты переходов из одних состояний в другие на одну временную ось, то случайные отрезки времени между ближайшими моментами будут представлять времена состояний системы Дг Время состояния системы характеризуется постоянством параметров состояний элементов системы и факторов или их изменением с постоянной скоростью. За случайный отрезок Дtc можно подсчитать все интересующие нас характеристики элементов и системы: наработку, время работы, время эксплуатации, время простоя по гшу фактору и время наложенного простоя. Двигаясь по оси времени от одного момента к другому и проводя суммирование временных характеристик и наработок, в е-е моменты времени можно подсчитать фактические текущие суммарные временные характеристики и наработки, а также комплексные показатели надежности и производительности элементов и системы.
Анализ схемы процесса функционирования ПС позволяет нрий — ти к выводу, что г-е время состояния системы отданного (£ -1)-го момента времени определяется как минимальное время из времен состояний элементов, рассчитанных от е го момента времени.
В общем случае время состояния элемента по тлму фактору определяем так:
При зависимости параметров v-го потока от производительности Q^
RQ?.ek /Qjoek — ССЛИ ХГ«к = 1 Л Ол ек >
FVik, если Xvck =0д П 03? = U
S,trm
М, если (Xwk = 1л = 0) v {Хшк = 0 л П «Л? ~> Xslm) = 0 (условие наступления квазистационарного состояния),
При независимости параметров т>го потока от производительности
Rtvek, если Хшк = 1 л П Kim Xolm ) = Ъ
Fvek, ССЛИ — 0 А П 03? Xt/7J = 1;
S,l.m
М, если (Х^ = 1 л П ОЙ -» ) = 0) V
V(Xvek = 0Д П ~~* ) = 0 (условие наступления квази
С / т стационарною состояния),
Где ХЫт, Xltn~ функции состояний Lm-та элемента но о- и л-факторам;
^oim ~ коэффициент прерывания работы или эксплуатации, или действия потока отказов, или заявок ек-го элемента но v-му фактору при
Вступлении в действие а фактора Im-vo элемента; Y^ — коэффициент прерывания простоя ек-го элемента при вступлении в действие 5-го фактора; М— временной интервал, значительно больший всех времен состояний элементов и принимаемый ориентировочно большим времени моделирования, т. е. М» ‘Г »
Значение М принимают времена состояний элементов но v-му фактору, находящихся в наложенном простое из-за а — и л-факторов, что устраняет выбор времени наложенного простоя, которое имеет неопределенный характер для данного элемента, в качестве времени состояния системы. Указанное состояние элемента можно охарак
теризовать как квазистационарное, являющееся неустойчивым для данного элемента, вызываемое внешними воздействиями и имеющее бесконечное время существования до тех пор, пока внешнее воздействие не приведет его в исходное состояние. В подобном состоянии может пребывать и уровень запаса полуфабрикатов в накопителях при их заполнении или опустошении.
Время состояния запасов полуфабрикатов в нако1 штеле Дt имеет вид
Ehi/QyhГ. еслиEkl>0AAQyhl <0; (EMhi -Eki)/AQ,yhi. если Ehi < Еш a AQyki >0; Af, если (Ehi = EMhl л ДQyht > 0) v (Ehi = 0 л ДQyki < 0) v vAQyhi = 0VQHkAI (условие наступления квазистационарного состояния),
&Qyhi =Q.yhi-Qyhi+h
Где Eh~ текущий запас полуфабрикатов в Hi—М накопителе; Е и — максимальная емкость hi-го накопителя; ЕтЫ— текущие производительности кг-ro участка и накопителя системы; М — время квазистационарного состояния.
На основе времен состояний элементов определяется время состояния системы как
V,e,K
Анализ текущих производи гелыюстей машин, участков и накопителей проводим после оценки функций состояний и скачка состояний элементов.
На первом этапе делается предварительная оценка текущих иро — изводительностей машин Q и участков AiB зависимости от их соб ственных состояний и факторов по формулам:
Qbij — ОнА,; П ~^ Xolm ) , (6.31)
Aji.ti Х ‘
С = в, оо, хр, н, и, м, ом, то, пр, рп, где Q, — номинальная производительность г-й машины J—RО участка K-й ветви; ХЫт — функция состояния 1пьто элемента по а-фактору;
|
Д’з Hi = |
|
Текущая номинальная производительность участка определяе гея как |
У^ ~ функция прерывания процесса работы Hij—Vi машины; о — причина простоя (фактор): в — восстановление; оо — ожидание об — сллокивания; хр — холодное резервирование; н — наладка; и — информационный простой; м — материальный простой; ом — обе луживание рабочего места; то — техническое обслуживание; пр — профилактический ремонт; рп — регламентированный перерыв;
|
|
|
|
Средняя номинальная производительность участка имеет вид
» = Ад, A SQЧь — SQlhi 4 d^Atc.
На втором этапе проводится анализ влияния на производительность г-го участка состояний других участков и накопителей, причем данный анализ проводим сначала по корневым ветвям, дкшаясь от первого участка к последнему, затем таким же образом по ствольным участкам, а потом в обратном порядке для учета влияния состояний последующих участков и накопителей на предыдущие.
Анализ в прямом и обратном порядке проводим по одним и тем же формулам:
QyM = °> если 4Hi = 1А Хи|кА, т О,
Qyh Ы = еСЛИ Ям = 1 Л ^внкА, =
Dyb — QyA,41 — если (ХвнкА|. = О A AQVAi > 0) v (EMfd — 0 a AQvhi >0)V
T8^.4i если (X^- = PA AQyhl <0)v(LMfl{ = 0A AQ_vfu <0)v
V(Јa,=0aa()ai.<0).
Затем следует пересчет нроизводительностей машин
|
|
Анализ текущих произи одительностей накопителей проводим по формулам:
ОлкЬ = 0, если ХвнкЛ1 = 0v bMhi = ОV(QyAi —ОАQyhи = 0)v
=£млг- а (Щы >0 л =0) v v(Јb=0A(QyM=0AQvA/+1>0;v V(qhi=0Л Ehi=EMhl AAQyftl>0)v
ОикЫ = Qyht. схли ftrOA(Jy/K>0)v
A AQv^<0)v >0 л Ehi < EMhi A A(Jvhi >0;
ВнкЛ, = QyA/+l. ^ЛИ (Ehl =0 A Clyhl <()) V v(^-=l A Eh=EMhi A AQyAf>0) V
V(Efu>Kki A ^/i>0A A(^y/„<0 ,
Где «у. — ключ на вид накопителя,
|
{ |
1, если накопитель транзитного типа;
0. если накопитель тупикового типа.
Номинальную производительность системы определяем равной минимальной из номинальных производителыюстеи участков, т е.
0нс = л = 1′ н—
H, Г
После оценки времени состояния системы следу ет определение текущих уровней запасов полуфабрикатов в накопителях Е и теку щего времени функционирования системы £как
T = t±Atc.
После этого следует оценка текущих сум марпых временных характеристик и наработок элементов и системы по факторам.
Для факторов, параметры которых зависят от производительности элементов и системы,
SIluek = + A/c ‘Оиек>
Mvek ~ SFvek " П (Ydm Xslm )0 ~ Xvek )>
S,l,m
А для факторов с параметрами, не зависящими от производительности,
SRvek = SR-uek + Д/с ■ П [ySm ~> ХА! т )>
Где Q^ — текущая производительность элемента при действии г>-го фактора.
Так, при действии потоков отказов машины и заявок на ее обслуживание Q^ = накопителей — Q^ = Q1kAi, при действии потока заявок на наладку Q, где Q —текущая средняя производительность системы.
Текущая суммарная наработка г-го участка определяется как
Коэффициент общего использования системы К (и текущую среднюю производительность системы рассчитываем по участку /, обладающему минимальной номинальной производительностью или номинальной производительностью системы, по формулам:
&
Следует иметь в виду, ч то коэффициент общего использования и производительность ПС, рассчитанные по формулам (б. ЗЗ), не учитывают освобождение накопителей от запасов изделий, которое производится после обработки тиража продукции перед наладкой, каждым режимным перерывом и профилактическими ремонтными работами, а также при материальных, энергетических и информационных простоях.
Для учета данного процесса следует отметить, что сброс остатков полуфабрикатов из накопителей осуществляется сразу же после остановки машин первого участка, поэтому в блоке анализа производи — тельностей участков необходимо обнулить производительности машин только первого участка главной корневой ветви при наступлении простоев по указанным факторам, а при расчете производится ь — ностей машин других участков следует исключить влияние перечисленных факторов на их производительность. Указанное условие обеспечивается, если в форму ле расчета производительностей для машин
Всех участков, кроме первого участка главной корневой ветви, под
Ставить индексы: о = в, оо, хр; г = 2, Пд, а в формуле расчета коэффи
Циента готовности ПС — /= А т. е, выработка ПС принимается равной выработке первого участка главной корневой ветви {SH = SR^j/i О гказы машин ПС могут сопровождаться выпуском бракованных полуфабрикатов и изде ши. Пусть количесг во бракованных изделий за один отказ X задано законом распределения Тогда текущее суммарное количество бракованных изделий, отсеивающихся после H/J-й машины,
Щц = srVjAl, +Щ(1-Xhij) П *am)K»hr
S,ltm
Текущее суммарное количество бракованных изделий, отсеиваю щихся после /гйчоучастка,
BRehi = X Srkfajy ;=I
А после ПС по видам полуфабрикатов
"уА
SR6ch = £ SR6hi>
Fi
Где п — количество участков на H—М пути ПС. По главному пуги ПС SRfc = SI^ Аг.
Тогда с учетом отсеивания бракованных изделий средняя производительность ПС будет иметь вид
А коэффициент общего использования ПС
* *
КОИ =0. /6нс-
Коэффициент выхода годной продукции (технологической готовности) с ПС можно определить как
Ктг — (Sl^ — SR&)/SRC,
*
Причем Кои = * *тг •
Наложенные простои, переданные на Лг-й участок другими участками, рассчитываем но формуле
ТШл Ы ~Щп /Он/и ~ SFhi>
Тогда коэффициент готовности ПС
~ ^нал Лг! )/(е ~ ^нал Лг1)
Или
Кс = (%1 /Си Brl)/(W Аг! /Он Arl + ^п)-
Предельную производительность ПС определяем равной производительности системы при условии EMhi —» т. е.
Qnc г = Ж = 1, Я.
Производительность жесткосблокированной Г1С определяем равной производительности системы, вычисленной при условии Е. —> оо, т. е.
MAI ‘
Сжс=(2с1^м/»=0, 2=1, па; Л = 1, Я.
Коэффициент насыщения производительности определяем по формуле
Алгоритм модели процесса функционирования ПС состоит из следующих этапов:
1- й этап — выбираются исходные данные и начальные условия;
2- й этап — проводится анализ состояний элементов ПС и скачков из одного состояния в другое;
3- й этап — определяются текущие производительности машин и накопителей;
4 й этап — определяются времена состояний элементов и системы;
5- й этап — определяются текущие уровни запасов полуфабрикатов в накопителях, текущее время моделирования, текущие суммарные наработки и времена простоев элементов по факторам, коэффициенты общего использования и готовности системы, производительность системы, коэффициент насыщения производительности системы, коэффициенты использования накопителей, коэффициент выхода годной продукции (технологической готовности);
6- й этан — проводится сравнение текущего времени T с заданным временем моделирования Т, но истечении которого выводятся конечные результаты, а также промежуточные результаты через время АТдля определения достоверности и точности результатов. В случае T< 7 имитационное моделирование продолжается с этапа 2.