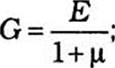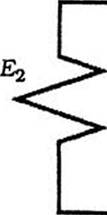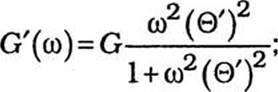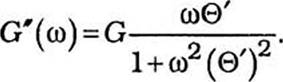(4.8)

(4.9)

Деформация полимеров имеет вязкоупругий характер. Наи­большее развитие в описании деформационных свойств поли­меров получила теория вязкотекучести, которая рассматрива­ет вязкоупругое тело как комбинацию идеально упругого и идеально вязкого элементов. Поведение идеально упругой со­ставляющей в терминах классической теории упругости выра­жается обобщенным законом Гука и характеризуется по край­ней мере двумя упругими константами — модулем Юнга Е и коэффициентом Пуассона ц. Другие константы — модуль упру­гости при сдвиге G и модуль объемного сжатия К— связаны с Ей [х следующими соотношениями:

(4.7)

Е

К= / — 3(1-2ц)

D = —; 1 = —. Е G

Где D и J— податливость при растяжении-сжатии и сдвиге со­ответственно. Сжимаемость

P-i н к

Поведение идеально вязкой составляющей деформации вы­ражают законом Ньютона для идеально вязкой жидкости и характеризуют вязкостью при сдвиге т).

Упругая деформация в твердом теле связана с деформацией валентных углов и связей между атомами. Поскольку отклоне­ния в дайнах связей и искажения валентных углов не могут быть большими, чисто упругая деформация по величине не может быть большой. При снятии нагрузки она мгновенно исчезает.

Природа эластической деформации связана с изменением формы макромолекул, обусловленной наличием определенной свободы вращения отдельных групп относительно валентных связей в главной цепи полимера при сохранении валентных уг­лов и длин этих связей. Эластические деформации могут быть большими. Они характеризуются ярко выраженным комплек­сом релаксационных явлений, при­водящих к постепенному их разви­тию и медленному исчезновению.

(4.10)

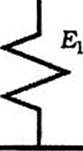
Рис. 4.6. Простейшая модель полимерного тела, Учитывающая упругие и эластические деформации

Многочисленные физические модели деформации полимеров под нагрузкой предусматривают моде­лирование упругой деформации пружиной с модулем Elt а эласти­ческой деформации — соединенны­ми параллельно пружиной с моду­лем Е2 и демпфером с жидкостью вязкостью ц2 (модель Кельвина — Фойхта-Мейера). Соединенные последовательно упругая пружина и эластический элемент Кельвина — Фойхта-Мейера моделируют упру­гую и эластическую деформации полимера (рис. 4.6) [2]. Полная де­формация такой модели составляет

A(T 1 1 ^ E(t)==—+ —fe 0 a(x)dT. (4.11)

EI Л20

Где т — текущее время; 0 — время запаздывания.

Параметр 0 соответствует времени, по истечении которого деформация в образце будет составлять (1—1 /е) часть от равновесной:

(4.12)

В частном случае при a = const соотношение (4.11) преобра­зуется в уравнение Александрова-Лазуркина

-t4 1-е0

A	A 4-
Ei	E2

8 =

(4.13)

Первый член этого уравнения отражает упругую часть де­формации, а второй — эластическую.

Следует заметить, что подобное моделирование позволяет представить механизм деформирования лишь в общем виде и не отражает всего комплекса сложных процессов, протекающих в полимере. Даже в области малых упругих деформаций модуль Юнга, моделируемый модулем упругости пружины Е}, непосто­янен. Измерение модуля Юнга на звуковых и ультразвуковых частотах при малых амплитудах динамической силы и дефор­мации с учетом изменения геометрии образца при его растяже­нии, т. е. в условиях, когда измеряемая величина Е отражает только упругую реакцию и подавлены эффекты, связанные с ре­лаксацией напряжения, показало, что при малых деформациях (до Е = 2-3%) модуль упругости убывает [26]. При деформациях более 3%, после перехода через «предел вынужденной эластич­ности», модуль начинает возрастать. На этих обоих участках из­менение модуля линейно связано с деформацией [13J:

Е В

Е = Е0 + Вг или — = 1 + —(4Л4)

Где Eq — «начальный» модуль Юнга; В — коэффициент измене­ния модуля Юнга.

Обычно вязкоупругие свойства полимеров исследуются в нескольких простейших режимах нагружения. Основные из них — переходные режимы ползучести и релаксации напря­жения, а также динамические режимы.

Под ползучестью понимают процесс нарастания во времени деформации в режиме постоянного истинного напряжения. Ползучесть проявляется даже у весьма жестких полимеров и обусловлена развитием вынужденно-эластических и пласти­ческих деформаций.

В режиме ползучести к образцу прикладывается напряже­ние о0. которое поддерживается постоянным в процессе испы­таний: а0 = const. Вязкоупругое поведение полимера выража­ется в том, что деформация е не сразу достигает постоянного значения (если оно существует), а возрастает с течением вре­мени по закону [48]

E(t) =

А0,

(4.15)

/0+ — + |f(t) Л2

Где /0 — мгновенная упругая податливость (I0 = 1 /Е0); T/R2 — Функция течения при произвольной длительности воздей­ствия о0; у (£) — функция ползучести, характеризующая нара­стание обратимой деформации. Учитывая, что

(4.16)

Где Јq — мгновенно развивающаяся начальная упругая дефор­мация, замеренная непосредственно в момент нагружения об разца, т. е. при T = О, уравнение (4.15) можно представить в виде

(4.17)

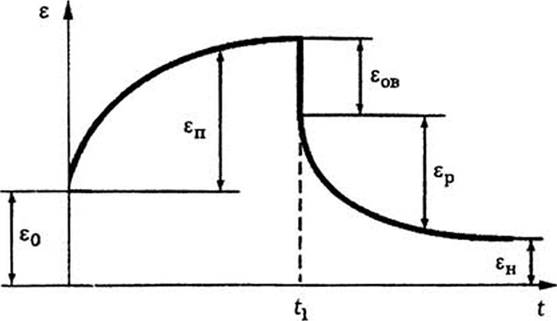
Где еп — деформация ползучести; вр = г^ — вынужденно-эласти­ческая деформация; ен — остаточная необратимая деформация.

После снятия напряжения а0 протекает процесс восстанов­ления образца — уменьшение деформации во времени. Дефор­мация практически мгновенно уменьшается на величину е0. Вынужденно-эластическая деформация уменьшается во вре­
мени (Ер = |/2 (£)), достигая равновесного значения при е = ен. Об­щий вид кривой ползучести и восстановления простейшей мо­дели полимерного тела показан на рис. 4.7.

В режиме релаксации напряжения испытания проводят при поддерживаемой постоянной деформации: еоп = const. Вследствие вязкоупругости среды напряжение, развивающее­ся в образце, постепенно уменьшается (релаксирует) по закону

ОП* (4.18)

Где Еж — равновесный модуль, равный отношению напряже­ния после завершения релаксации к начальной деформации; Ф (£) — функция релаксации; T — заданное время, отсчитывае­мое от момента начала нагружения.

Монотонно убывающую функцию ср (t) и монотонно возра­стающую функцию у (t) обычно выражают в виде

TOC o "1-3" h z ОО *■*£ ОО "I

Cp(t) = JF(0′)e^d0′, 4/(O = J/(0)e0d©, (4Л9)

О о

где 0и0′ — время запаздывания и релаксации; /(О) и F(0′) — функции распределения времени запаздывания и релаксации.

При представлении релаксационных данных наиболее рас­пространена логарифмическая шкала времени, поэтому обыч-

Рис. 4.7. Схема зависимости деформации от времени при постоянном напряжении

Но функции F(@’) и/(©) заменяют функциями Н[&) = 0′ F(Q’) и L(0) = 0/(0). В этом случае формулы (4.19) записываются сле­дующим образом:

-t 1-е®’

/

Оо

<P(0 = JH(©’) О

Оо

Din©’, v(t)=jL(0)

-t

Din©. (4.20)

1-е0

О

В теории линейной вязкоупругости к полимерам применим принцип временной суперпозиции Больцмана, а деформации (или напряжения) связаны с предысторией нагружения (или деформирования) уравнением Больцмана-Вольтерры:

Da(x)

(0=]

Dx,

Dx

/о + t—+ v(t-x)

—СО

(4.21)

В режиме динамических испытаний задают изменяющиеся по гармоническому или затухающему закону с частотой со де­формации или напряжения и определяют частотные зависи­мости действительных (G’ и Г) и мнимых (G" и Г) составляю­щих комплексного модуля упругости G* (со) и комплексной по­датливости Г (со):

G*(co) = G'(o))+iG'(a)),

Г(«)—JL-.

(4.22) (4.23)

G (со)

Эти характеристики могут быть выражены через релакса­ционный спектр материала:

0

О)©’

D&.

(4.24)

1 + ы2(0′)2

ОО

G»=jF(0′)

О

Действительная составляющая комплексного модуля упру­гости G’ (со) называется динамическим модулем упру гости. Он характеризует величину накопленной в теле упругой энергии. Мнимая часть комплексного модуля G" (со) называется моду­лем потерь и характеризует потери механической энергии на вязкое трение, связанные с рассеянием энергии при упругих и эластических деформациях. Механические потери в вязко — упругом теле обычно характеризуют тангенсом угла механи — ческйх потерь tg 5, коэффициентом поглощения ап или декре­ментом затухания D:

2па Со

(4.25)

TgS=Ј; D =

И со

СО

(4.26)

(4.27)

Функции ф (£), |/ (£), G’ (со), G" (со), а также константы /0, т]2. EL называют основными реологическими характеристиками вязкоупрутих материалов. Они определяются релаксационны­ми свойствами материала и могут быть выражены через функ­ции распределения времен релаксации и запаздывания. По­этому все реологические характеристики не являются незави­симыми, а связаны между собой математическими соотноше­ниями. В наиболее простой форме эти соотношения имеют следующий вид [38]:

-t

Gp(t) = Ge&;

In(t) = I 1-е0′ ;

(4.28)

(4.29)

Качественной характеристикой деформационных свойств яв­ляется понятие жесткости (мягкости) материала. К жестким обычно относят полимерные материалы, имеющие модуль Юнга Е> 103 МПа. При Е< 103 МПа материалы считаются мягкими.

Влияние температуры на реологические характеристики связано с температурной зависимостью времен релаксации:

-дБ

& = t0e*r. (4-3°)

Где t0 — константа; ЛЕ— энергия активации; R — универсаль­ная газовая постоянная.

В случае релаксационных переходов, связанных с повыше­нием температуры динамических испытаний, на кривой тем­пературной зависимости G наблюдается перегиб, а на графи­ках температурных зависимостей G" и tg 5 — максимумы. При этом частота со связана с температурой релаксационного пере­хода Тр зависимостью

ЛЕ

Into =

RTp‘ (4-31)

Е-Л.

(4.32)

Отношение времен релаксации при температуре Т и выб­ранной «стандартной» температуре Т0 называют фактором сдвига или температурным коэффициентом сдвига с^:

В'(Т)

Коэффициент сдвига является универсальной функцией температуры и выражается уравнением Вильямса-Лэндела — Ферри (ВЛФ)

1еа _ С^Т-Тр)

Где С1иС2 — постоянные, зависящие от Т0.

Принцип температурно-временной суперпозиции устанав­ливает эквивалентность влияния на реологические характери­стики временных и температурных условий нагружения. Ис­пользование метода приведенных переменных позволяет зна­чительно расширить температурный и временной интервалы исследуемых характеристик без проведения дополнительных экспериментов.

ТАРА И ЕЕ ПРОИЗВОДСТВО

Типы сварных соединений и швов

Основными типами сварных соединений полимерных пленочных материалов являются стыковое, нахлесточное, Т-образное и угловое. Помимо геометрической характерис­тики способа сопряжения поверхностей тип сварного соеди­нения характеризует и форма кромок соединяемых деталей. Кромки могут быть прямыми, с односторонним или двусто­ронним скосом. Сварные швы характеризуют способом выполнения сварки, технологическими и конструктивными особенностями: одно­сторонняя или двусторонняя сварка, наличие одной или двух […]

ТАРА И ЕЕ ПРОИЗВОДСТВО

Ефремовы. Ф. Двадцатый век характерен бурным развитием науки и тех­ники. Как следствие, во многих отраслях промышленности пе­риодически возникают новые профессии, о которых раньше было трудно даже предполагать. По уровню производства ко­нец XX столетия несопоставим с началом и даже с серединой столетия. Поэтому совершенно естественным являются требо­вания к подготовке инженеров новых специальностей. По сво­ей сути инженеры […]

Биговка

Биговкой называют предварительное нанесение на мате­риал линий сгибов (бигов) в виде выдавленных канавок опре­деленного профиля. Биговка предназначена для снижения жесткости листовых заготовок по линии сгиба. Она значительно облегчает условия образования сгибов и является эффективным средством повы­шения качества складных коробок, особенно в условиях авто­матизированной сборки. Биговка представляет собой процесс местной вытяжки ма­териала и осуществляется по следующей […]