Решим задачу СМО, приведенную в примере 4, с использованием системы MathCAD.

Ввод текста на всех этапах решения задачи осуществляют с помо­щью комбинаций клавиш «Shift + "» , что позволяет создать тексто­вую область. Введем на рабочем листе первый пункт расчета:

1. Задание исходных данных.

Затем последовательно введем исходные данные в поле экрана (рис. 6.18):

X -0.25 ц :=0.33 п ~2

Для решения задачи воспользуемся блоком функций Given…Find, Для этого необходимо задать начальные приближения. Введем на рабочем листе второй пункт расчета:

Y. Задание исходных данных: X := 0.25 Ji :=0 ВВзЗГ"

2. Начальные приближения. РО :=0 2Ь PI :Ч).25 Р2 :=0.25 РЗ :=0 25

3. Запись системы уравнений, описывающей функционирование многоканальной СМО

Given

—X-?Q + I Р1 = 0 А-Р0-(А + ц)-Р1+2-й Р2-0 А-Р1-(Я. + 2 [х) Р2н ЗцРЗ = 0 Р0+Р1+Р2+Р3 = 1

‘ИЛ Р1 Г2

Л

4. Результаты решения — РО = 0.476 Р1 и 0.357 Р2 = 0.134 РЗ = 0.033

Рис.. 6. IS Определение параметров функционирования многоканальной замкнутой

СМО с отказами в системе MaihCAD

2. Начальные приближения

Затем последовательно введем начальные приближенные значе­ния искомых парамет-ров:

Р0:=0.4 Р1-0.2 Р2:=0.2 РЗ-0.2

Введем на рабочем листе третий пункт расчета.

3. Запись системы уравнений, описывающей функционированиемногока нальнои СМО.

Вначале вводим ключевое слово С Yen (Дано), которое может быть напечатано прописными, строчными буквами или начинаться с про­писной, затем исходную систему уравнений с жлрныч «=», а в зак­лючение — вектор искомых величин. Для этого в ноле рабочего листа определяем местоположение вектора. Если в окне выведена панель инструментов Math (Математика), нужно щелкнуть но кноп­ке с изображением матрицы. Появится аналоговое окно Matrix (Матрица). Здесь щелкаем по кнопке с аналогичным изображени­ем или нажимаем комбинацию клавиш «Ctrl + М». В обоих случаях появится диалоговое окно Insert Matrix (Вставить матрицу). В его текстовых полях Rows (Строки) и Columns (Столбцы) вставим нуж­ное число ст рок и столбцов в нашей задаче 4 и 1 соответственно. После щелчка по кнопке ОК появится шаблон с метками для ввода искомых данных, Подводя курсор или указатель мыши к каждой из

Них, зададим искомые параметры, затем знак присваивания и имя встроенной функции Friid(P0,Pl, P2,P3,P4,P5). Выведем на рабочий лист четвертый пункт расчета: 4. Результаты решения.

Для получения результатов расчета искомых величин достаточно набрать имя H)Oki Юго параметра и знак J >авенсгва, па жав соо гветс гвук>- щук > клавишу или щелкнув по кнопке со знаком равенства, расположен­ной в верхнем левом уг. ту панели инструментов Evalu… (Вычисления;.

Рассмотрим неустановившийся режим работы СМО когда ее ос — н овные характеристики завися г от времени В этом случае функцио­нирование СМО будем описывать системой обыкновенных диффе­ренциальных уравнений:

#h=-(A] *-ix)P](t) + }.PQ(t) + 2iiP2(t), Щ = -(к+2хЩ (0 + XPl(t) + ЗцР, (/),

P‘{t)=-здею(6.113)

На рис. 6.19 представлены исходные данные и система дифферен­циальных уравнений, описывающая функционирование многоканаль­ной замкнутой СМО при неустановившемся режиме работы.

1 Задание исходных данных многоканальной замкнутой СМО с отказами при неустановившемся режиме.

X := 0 25 ц := 0 3333

2 Система обыкновенных дифференциальных уравнений, описывающих функционирование многоканальной замкнутой СМО с отказами

Ip0(t)=-x-po(t)+li-p1(t) dt

TlltJHP P0(t)-(X +м) Pi(t) + 2-M. P2(t) dt

Dt

^{t)=A. p2(t)-3.M. p3(0

Pile. 6.19. Олисание функционирования многоканальной замкнутой СМО

При неустановившемся режиме

На рис. 6 20 показаны правые части системы уравнении в виде вектор-столбца. Каждый его элемент определяет значение правой части соответствующего дифференциального уравнения на любом шаге ин гегрирования (решения). Здесь же даны начальные значения искомых параметров в виде вектор — столбца. В нижнеи части рисунка определены начальное и конечное время интегрирования и число шаг ов решения системы дифференциальных уравнений.

3 Формирование функции, которая определяет вектор отклонений искомых величин D(t, Р) и векгор начальных значений Р.

4. Определение дополнительных параметров для решения системы обыкновенных дифференциальных уравнений" начальное и конечное время исследования системы и число тагов интегрирования t0 := 0 tl := 6 N := 1000

Рис, 6 20. Представление системы дифференциальных уравнений в виде, доступном

Для решения ее в системе MathCAD

На рис. 6.21 приводится решение системы дифференциальных уравнений многоканачьнои замкнутой СМО с использованием встро­енной функции Rkfixed(P,TO,Tl,N,D), реализующей метод Рунге — Кут — та с фиксированным шагом. Для вызова этой функции необходимо: щелкнуть по пункту Insert (Вставка) главного меню, а затем по пун­кту Function (Функция) падающего меню или нажать комбинацию клавиш «Ctrl + Е» Появится диалоговое окно Insert Function (Вста­вить функцию):

Паити в разделе Function Category (Категория функции) строку Differential Equation Solving (Решение дифференциального уравне­ния) и щелкнуть по пей левой кнопкой мыши. В правом поле в разде­ле Function Name (Имя функции) появится список функций для ре­шения дифференциальных уравнений;

Найти в списке функцию Rkfixed и щелкнуть по ней мышью. После этого щелкнуть по кнопке ОК. В месге установки визира появится шаблон функции для решения системы уравнений ме­тодом Рунге-Кутга.

5. Решение системы обыкновенных дифференциальных уравнений с использованием встроенной функции rkhxed(P, tO, tl, N,D).

S:=rkfixcd(P, tO, tl, N,D) t:=S<0) PO:=S(1) PL=S<2> P2:=S<3> P3:=S<4>

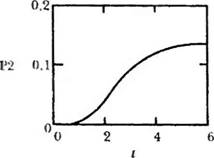
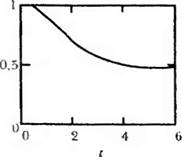
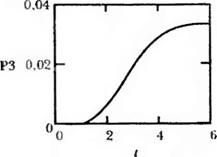
6. Представление результатов решения в графическом виде.

Рис. 6.21 Решение системы дифференциальных уравнений, описывающих функционирование многоканальной замкнутой СМО с отказами

Можно сразу найти функцию rkfixed в правом поле раздела Function Name, после чего щелкнуть мышью по ней, а затем по кноп­ке ОК, но это займет больше времени. В обоих случаях в нижних по­лях диалогового окна будет дано правильное обозначение выбранной функции со всеми аргументами, а также краткое описание ее действий. На рис. 6.21 приведено графическое решение системы дифференци­альных уравнений для первых двух искомых параметров, т. е. представ­лено поведение параметров РО, PI, Р2 и РЗ — вероятности отсутствия требований и наличия в системе одного, двух и трех требований со­ответственно в зависимости от длительности процесса.

Анализируя графическое решение системы обыкновенных диф — фс ренциальныхуравнений, описывающей функционирование задан­ной многоканальной замкнутой СМО, можно заметить, что пример­но через 0,2 ч она переходит в установившийся режим работы. При этом значения вероятностей состояний режима работы системы при решении совокупности обыкновенных дифференциальных уравне­
ний практически полностью соответствуют решению системы алгеб­раических уравнений для установившегося режима работы.

СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ УПАКОВОЧНОГО ПРОИЗВОДСТВА

Использование специализированных САПР в допечатной стадии производства упаковки

Важным этапом произволе тва упаковки является доиечатный про­цесс. Качество готовой упаковки в значительной степени определя­ется допечатной стадией — дизайном. Можно утверждать, что конку­рентоспособность производителя полиграфической продукции оп­ределяется уровнем дизайна, который не в последнюю очередь зави­сит от программ ных с редств. Ксли вспомнить эволюцию систем допечатной подготовки, то можно отметить следующие закономерности Вначале применялись закрытые системы […]

Симплексный метод

Геометрическая интерпретация симплексного метода. В т еории линейного программирования рассмотрены основные теоремы ли­нейного программирования, из которых следует, что если задача ли­нейного программирования имеет оптимальное решение, то оно со­ответствует хотя бы одной угловой точке многогранника решений и совпадает по крайней мере с одним из допустимых базисных реше­ний системы ограничений. Там же указан путь решения любой зада­чи […]

Математическое обеспечение подсистем машинной графики и геометрического моделирования

Изучение математического аппарата, лежащего в основе машин­ной графики и проектирования геометрии упаковки, начнем с рассмот­рения способов вывода и преобразования точек и линий. Эти спосо­бы наряду с соответствующими алгоритмами рисования используют­ся для изображения объектов или визуализации графической инфор­мации. Возможность проводить преобразования точек и линий явля­ется фундаментом машинной графики. Нарисованный объект может быть представлен в нужном масштабе, […]