Представление кривых
Существует множество способов построения кривых вручную с помощью карандаша, ручки, кисточки, ножа и разнообразных инструментов: линейки, лекала, циркуля, плаза, шаблона и т. д. Каждый инструмент служит определенной цели, причем нет пи одного абсолютно универсального. Точно так же в машинной графике кривые строятся с помощью разных методов и инструментов.
Кривая может быть представлена совокупностью точек. Если точки расположены близко друг от друга, то, соединяя их отрезками прямой, мы получим изображение кривой. Точки на кривой можно расположить равномерно по ее длине. В результате получается довольно плохое представление кривой, особенно если мал радиус кривизны. Улучшить вид кривой можно, увеличивая плотность точек в таких участках.
Хотя кривые могут быть достаточно хорошо представлены совокупностью точек, аналитическое представление во многих отношениях предпочтительнее. Его преимущества — это точность, компактность записи и простота вычисления промежуточных точек. Аналитическое представление позволяет без труда определить наклон и радиус кривизны, а при точечном представлении для этого требуется численное дифференцирование — чрезвычайно неточная процедура. Сравните объем памяти для точечного представления окружности с 32 точками на ней и аналитическое представление — координаты центра и радиус.
При аналитическом представлении кривой молено точно определить положение любой точки, а при точечном нужна интерполяция, причем в общем случае результат интерполяции не принадлежит кривой.
Опыт показывает, что аналитически представленные кривые легче изображать на рисунке. Аналитическое представление выгоднее, когда для удовлетворения заданному критерию необходимо непрерывно изменять форму кривой.
Часто требуется аналитическое представление кривой, первоначально заданной точками. Для того чтобы провести кривую через все заданные точки, применяется метод кусочной полиномиальной аппроксимации. Для этого требуется определить коэффициенты полинома некоторой степени. Вид кривой в промежуточных точках зависит от степени полинома и граничных условий.
Если же точки — только приблизительные значения величин, например данные экспериментальных измерений или наблюдений, то нужна кривая, задающая верное направление изменения В общем случае кривая может не проходить ни через одну точк) данных. Здесь применяется метод наименьших квадратов. Этот метод дает кривую в виде у =f{x), которая минимизирует сумму квадратов отклонений по оси у между данными и полученной кривои. Вид у = J[x) выбирают, исходя из характера изучаемого процесса.
Обычно для метода наименьших квадратов используются полиномы, линейные, степенные и окспоненциа аьные функции. Независимо от выбора вида кривой метод требует решения системы линейных ал гебраических уравнений для определения неизвестных конст ант.
Непараметричсские кривые. Математ ически кривая может бы гь представлена в параметрической или непараметрической форме. Непараметрическая кривая задается в виде явной или неявной функции. Для плоской кривой явное неиараметрическое представление имеет вид: y~jlx). Одному значению л: соответствует только одно значение у, поэтому замкнутые или многозначные кривые, на пример окружность, явно представить нельзя. Неявное представление j{x, У) = 0 позволяет обойти это ограничение.
Как явное, так и неявное непараметрическое представление осе — зависимо, т. е. сложност ь обработки зависит от выбора системы координат. Например, если в заданной системе координат граничным условием является вертикальный наклон, нужно либо изменить ее, либо аппроксимировать бесконечный коэффициент наклона наибольшей допустимой положительной или отрицательной величиной.
Кроме того, если точки на осезависимой непараметрической кривой вычисляются с равномерным приращением по хили у, они не будут равномерно распределены вдоль кривой. Это может повлиять на качество и точность графического изображения. Тем не менее непарамет — рическое представление бывает полезным. Теперь рассмотрим параметрическое представление, позволяющее обойти эти ограничения.
Параметрические кривые. В параметрическом виде каждая ко ордината точки кривой представлена как функция одного параметра. Значение параметра задаст координатный вектор точки на кривои. Для двумерной кривой с параметром ^координаты точки равны
Х= x(t),y = y(t).
Тохда векторное представление точки на кривой
Л’И*8 уШ.
Чтобы полупить непараметрическую форму, нужно исключить T Из двух уравнении и вывести одно в терминах х и у.
Параметрическая форма позволяет представить замкнутые и мно — гозначные кривые. Производная, т. е. касательный вектор, есть
Так как точка на параметрической кривой определяется только значением параметра, эта форма не зависит от выбора системы координат Конечные точка и длина кривой определяются диапазоном изменения параметра. Часто бывает удобно нормализовать параметр на отрезке кривой к 0 < T< 1. Осенезависимость параметрической кривой позволяет с легкостью проводить с ней аффинные преобразования.
Самое простое параметрическое представление у прямой. Для двух векторов положения Р и Р2 параметрический вид отрезка прямой между ними такой:
P{t) = P1+(P2-P})2, 0<*<1.
Так как P(l) — это вектор, у каждой его составляющей есть параметрическое представление x(t) и y(t) между Р] и Р2:
X(t) = x^ + (x2-xi)t-,
Параметрическое представление окружности Параметрическое представление окружности радиуса г с центром в начале координат:
Х = г cosa; у= г sina, 0< а< 271.
Где а — параметр.
Полной окружности соответствует диапазон изменения параметра а от 0 до 271. Равномерное приращение параметра а дает хорошее изображение окружности, поданный алгоритм неэффективен из за частого вызова тригонометрических функций.
Нижеприведенный алгоритм дает лучшие результаты по времени вычислений.
Если рассматривать некоторое фиксированное число равномер но распределенных точек по окружности, то приращение параметра между точками можно считать константой. Координаты любой точки на окружности с центром в начале координат
Х = rcos(a + Да); yrtl = rsm(ai + Aa).
По формуле суммы углов
= r(cosCt, cosAa — sina sinAa); у = r(cosa(sinAa + sina cosAa).
Воспользуемся тем, что для a = a
Л: = г cos a;
TOC o "1-3" h z I г
У = rsina, 0<a <2,
-I I r
И получим рекурсивные у равнения
Х, = х cosAa — — у sinAa;
/»1 I У i ‘
У = х. sinAa + у. cosAa, что соответствует повороту точки (х., у.) на Аа.
Так как Аа постоянно и равно 2п/(п — 1), где п — количество равномерно распределенных но окружности точек, значения sin и cos нужно вычислить только один раз. Во внутреннем цикле используются только четыре умножения, вычитание и сложение, поэтому алгоритм работает очень быстро.
Стандартное параметрическое представление единичной Окружности имеет вид
Х = cosa; У = sina, 0 < a < 2П.
Следующее параметрическое представление также имеет вид дуги единичной окружности в первом квадранте:
ДО в 1X0 ><03 = [(1-0/(1 + О 2£/(1 + 0]. 0<f<i.
Окружность с центром в произвольном точке получается переносом окружности соответствующего радиуса с центром в начале координат. В некоторых случаях можно упрост ить задачу: сначала строить единичную окружность с центром в начале координат, а затем, комбинируя перенос и масштабирование, получить окружности с любым радиусом и центром.
Параметрическое представление эллипса. Стандартное представление эллипса с центром в начале координат, большой полуосью А и малой полуосью B имеет вид
Х = a cosa;
У = B sina. 0 < a < 2п (6.1 ] 5)
Если рассчитывать точки эллипса через равные приращения угла, изображение будет неверным. Особенно сильно неточности проявляются на концах, где кривизна слишком велика и требуется большое количество точек.
Если задано фиксированное количество точек на эллипсе, мож но, пользуясь формулами суммы углов, получить эффективный алгоритм. Координаты любой точки на эллипсе:
Х = «cos(a + Да);
= Да),
Где Да = 271/(п — 1) — фиксированное приращение а; п — количество точек на периметре; at — значение параметра для х. и у.. По формуле суммы углов
Х^ = a (cosat cosAa — sina( sinAa); у^ = b( cosa_ sinAa+ sinat cosAa). (6.116)
Используя (6.115), перепишем уравнения (6.116): x^j = x cosAa — (a/b) у. sinAa;
Y.+1= (b/ a)x, sin Aa + y. cosAa. (6.117)
Чтобы получить эллипс с центром не в начале координат и с главной осью, расположенной под углом к горизонтали, сто поворачивают вокруг начала координат, а затем переносят.
Как видно из системы уравнений (6.117), окружность является частным случаем эллипса при а = к
Пространственные кривые. Трехмерные или пространственные кривые широко используются в проектировании и разработке самой различной упаковочной продукции: бутылок, банок, коробок и т. д.
До начала применения математических и компьютерных моделей в процессе производства, дизайна и изготовления их использовалась начертательная геометрия. Многие ее методы были перенесены в машинную графику.
Поверхности часто изображаются как сеть кривых, лежащих в ортогональных секущих плоскостях, с трехмерными контурами деталей. Сечения получаются оцифровкой физической модели или чертежа и математическим подбором кривой, проходящей через все заданные точки. При этом используются два таких метода: кубические сплайны и параболическая интерполяция. Существуют и иные реализации этого подхода.
Другой подход состоит в том, что математическое описание кривых генерируется без изначального знания формы кривой. Его примеры — кривые Безье и их обобщение до В-сгшайнов. Эти методы отличаются тем, что кривая может не проходить ни через одну заданную точку. Контрольные точки определяют только направление изгиба.
Трехмерные кривые можно представить параметрически или непараметрически. Явное непараметрическое представление имеет вид
X=x,y=J{x),z= g(x).
Неявное ненараметрическое представление кривой как пересечения двух поверхностей задается уравнениями:
/х, у, z) = 0, g(x, У, z) = 0.
Общий параметрический вид пространственной кривой можно записать в виде
Х — *(t),y = y(t), z=z(l). Где параметр / изменяется в определенных пределах < T < Tr
В приведенном выше явном непараметрическом представлении х можно рассматривать как параметр, х= L Тогда этаже кривая имеет нараметричес кую форму
Х=/,у=Д0, z = g{t).
Кубические сплайны. В промышленном производстве, например судо-, автомобиле — и авиастроении, окончательная форма в реальном или близком к нему масштабе определяется в процессе доводки.
Ав гоматизация этого процесса представляла значительный интерес для машинной графики Формл математического сплайна повторяет контур физи ческого сплайна, г. е. гибкой деревянной или пластмассовой линейки (рейки), проходящей через определенные точки. Для изменения формы сплайна используются свинцовые грузики. Меняя их количество и расположение, получившуюся кривую стараются сделать более гладкой, красивой и «приятной для глаза >.
В общем случае математическии сплайн — это кусочный полином степени к с непрерывной производной степени к — 1 в точках соединения сегментов. Гак, кубический сплайн имеет в точках соединения непрерывность второго порядка. Кусочные сплайны из многочленов невысокого порядка очень удобны для интерполяции кривых, так как они не требу ют больших вычислительных зат| >ат и не вызывают численных отклонений, свойственных многочленам высокого порядка. По аналогии с физическими сплайнами обычно используе гея серия кубических сегмент ов, причем каждый сегмент проходит через две точки. Кубический енлайн удобен еще и тем, чт о. это кривая наименьшего порядка, допускающая точки перегиба и изгиб в пространстве.
Уравнение одного параметрического сегмента сплайна
P{T)=*$M/- <,<-<■*. (6.118)
I-i
Где I и t — значения параметров в начале и конце сегмента; P(t) — Вектор к любой точке сегмента.
В случае декартовых координат
Я0 = [п*) y(t) z(t).
В цилиндрической системе координат
P(t)=[3 B{t) 2(0], где r(t), 9(/), 2(0 — компоненты цилиндрической системы координат
Каждая составляющая имеет вид, похожий на P(t), т. е.
У«)=й V1‘ 0 =
Г=1 T<t<l2.
ГГосчрднныс коэффициенты В вычисляются исходя из четырех граничных условий для сегмента сплайна. Запишем уравнение (6 .118) в виде
Д0 = +V’ (бЛ19)
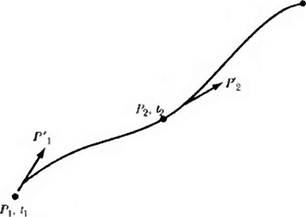
Пусть Р} и Р,— векторы концов сегмента (рис. 6.22). Пусть также Р и Р производные по T, будут касательными векторами в концах сегмеша. Дифференцируя уравнение (6.118), получим
P‘(t)= [xt) I(t) zl)]=iBi(t-iy-2, tx<t<t2.
I=l
Запишем результат:
Предположим, без потери общности, что L = 0, и применим граничные условия:
ДО) = Pi, ДО = Р2, Р'{0) = Р, 4ЩЦ = Р’г.
Получим четыре уравнения для неизвестных В :
Р{0) = В = Р ; ‘ (6.120)
Д Q = ^ + Н В, Q ;
Решения для В и В имеют вид:
Л, 3(Р2 — Я,)/^ — 2РД — К/1,; (6.122)
Д4 — 2(Р, — Я2)/<2′ + Р / + Р. г . 16.123)
Величины В. у В, В^ и задают сегмент кубического сплайна. Очевидно, что форма сегмента зависит от положения касательных векторов в концах сегмента. Далее, заметим, что в результатах присутствует значение параметра T— T2 в конце сегмента. Так как каждая конечная точка и вектор касания имеют гри компоненты, параметрическое уравнение ю бической пространственной кривой зависит от двенадцати векторных компонент и значения параметра t2 в конце cei мента.
Чтобы построить кривую целиком, нужно соединить множество сегментов — На рис. 6.23 показаны два соседних сегмента.
Г’,
Р
Г
Риг 6.23. Один сегмент кубического сплайна
Если известны векторы Р, Р, Р, касательные в< кторы Р’, Р’, Р’ и значения параметров lr t. s (рис. 6.24), то форма каждого сегмента определяется из уравнения (6.119) Однако маловероятно, что известен касательный вектор Р’ в точке соединения. Его можно вывести из условия непрерывности.
Л-Н __
|
Рис. 6.24. Два кусочно кубических сегмента сплайна |
Вспомним, что кусочный сплайн степени к имеет непрерывность степени к-1 в точках соединения; непрерывность кубического сплайна равна двум. Для этого должна быть непрерывна вторая производная Р" (А пли кривизна линии. Дважды продифференцировав урав ненке (6 118), получим
P‘(t)-lxV) yV) = 1)(г- tx <l<t2. (6 124)
I=l
Для первого куска сплайна параметр изменяется в пределах О <t< T2. Подставим t = t в уравнение (6.124).
|
/ РЛ л2 |
4 Р"=ЪВА12 + Щ.
Для второго участка сплайна параметр изменяется в диапазоне О <t<1Ъ к Подставим в уравнение (6.124) значение /= 0 в начале второго участка
Р" = Щ.
Приравнивая полученные результаты и пользуясь равнениями (6.120)-(6.122), будем иметь
6^[2(P, — Р2) А/+Р/Q+Rwt + — р})м — 2Ц д — к т =
= 2 [ЦР, — M/Q — 2 р; /<, — р; /д. (6.125)
Левая чаегь этого уравнения представляет кривизну в конце пер вого сегмента, а правая — в начале второго. Умножим обе части уравнения (6.125) на t2t$ и сгруппируем члены:
/Зр; +2(^ + ypg + Lp; =з[/21!(р3-р?)^^(р2-р1)]/(у3) (6.126)
Отсюда определяется Р ~ неизвестный касательный вектор в точке соединения. Отметим, что в окончательном уравнении опять присутств^т значения параметра T в концах cei ментоь (2 и.
Формулу можно обобщить для п точек, и для 72-1 сегментов кубического сплайна получить непрерывность второго порядка в точках соединения.
Кривые Безье. Существует класс задач, когда решение зависит как от функциональных, так и от эстетических требований, например дизайн поверхности мебели, посуды или упаковки. Кроме количественных критериев здесь требуется учет практического опыта, и часто необходимо интерактивное вмешательс гво разработчика.
Рассмотренные выше методы, в частности кубические сплайны, неудобны для интерактивной работы. Направление и величина касательных не дают необходимого интуитивного представления о кривой, так как неочевидна связь между набором чисел и формой соответствующей кривой.
Пьер Безье предложил друг ой метод создания кривых и поверхностей любой ф( >рмы. Безье вывел математическу ю основу своего метода из геометрических соображений, но его результ ат эквивалентен базису Бернштеина или функции полиномиальной аппроксимации.
Кривая Безье задается многоугольн иком, как показано на рис. 6.25. Так как базис Безье является бернштейновским, сразу же известны некоторые свойства кривых Безье, например:
Функции базиса вещественны.
Степень многочлена, определяющего участок кривой, на единицу меньше количества точек соответствующего многоугольника. Основа формы кривой повторяет очертания многоугольника. Первая и последняя точки кривой совпадают с соответствующими точками определяющего многоугольника.
Векторы касательных в концах кривой по направлению совпадают с первой и последней сторонами многоугольника.
Кривая лежит внутри выпуклой оболочки многоугольника, т. е. внутри самого большого многоугольника, построенного но заданным точкам.
Кривая обладает свойством уменьшения вариации. Это означает, что кривая пересекает любую прямую линию не чаще, чем определяющий многоугольник.
Кривая инвариантна относительно аффинных преобразований.
|
Рис. 6.25. Кривая Безье и определяющие ее точки |
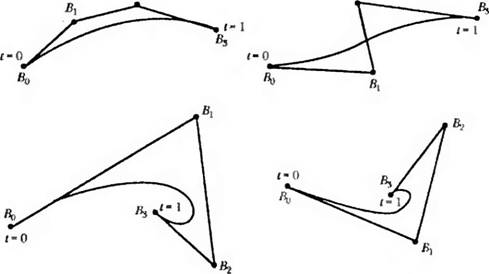
На рис. 6.26 показано несколько четырехточечных многоугольников Безье и соответствующих кривых. На основе перечисленных выше свойств можно легко научиться предсказывать форму кривой по виду многоугольника.
К2
|
Рис. 6.26. Многоугольники Безье для кубических кривых |
Математическое параметрическое представление кривой Безье имеет вид
/Ч0=ХЧЛ;Ю. О<1<1, (6.127)
Г=0
Где базис Безье или Бернштейна (функция аппроксимации)
П
Г
|
П-г |
|
(6.128) |
У
|
У1 J |
П
I{n — i)
|
(W |
Г Г |
|
|
I V J |
1 |
|
3! |
|
Г!(3-1)!’ Ai (0=ЗД-0*; АО = + A A, + &Jv2 + As = Коэффициенты для кривои Безье |
Рассмотрим построение кривои Безье на примере. Пусть заданы вершины прямоугольника Безье: Л()[1 1], В{[2 3]; В2[4 3]; В%[Ъ 1]. Найти семь точек, лежащих на кривой Ьезье. В нашем случае п = 3, так как имеется четыре вершины. Отсюда
Итак,
|
Таблица 6.5
|
Значения^ для различных значений T приведены в табл. 6.5. Точки на кривой: Р(0)=В1Г[ 1];
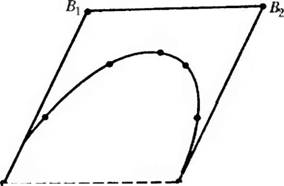
ДО, 15) =0,614 Bi + 0,825 В{ + 0,058 Д, + 0,008 Bs = [1,5 1,765]; Д0,35) = 0,275^’+ 0,444Я + 0.239Д, + 0,042 = [2,248 2,367]; ДО,5) =0,125 Вп + 0,375 В1 + 0,375 В, + 0,125 1% = [2,75 2,5]; ДО,65) = 0,042До + 0,239 Д, + 0,444 В2 + 0,275В.} = [3,122 2,367]; Р(0,85) = 0,003 В0 + 0,058Bj + 0.325Д, + 0,614Л, = [3,248 1,765]; Д1) = /?3 = [3 1].
Эти точки показаны на определяющем многоугольнике на рис. 6.27.
|
Рис. 6.27. Сегмент кривой Ьезье |
|
Fio * |
Уравнение кривой Безье можно записать в матричном виде, так же как уравнения для кубических сплайнов и параболическом интерполяции:
P(l) = TNG= FG, Здесь 7 = [Г г’ … 1 1], / = Ц,.0 Л, … /,.„], С — [В0 Вх … Я],
|
H |
Fn" |
|
|
-n |
||
|
V J |
V |
/ |
|
(-1)’ |
|
ПУп-1 1 п-1 |
|
О |
|
П-1 |
|
1-1 г НГ1 |
|
(-1) |
|
0 |
|
/г |
|
Ч Г пУ п-1 1 п-2 |
|
Ч П Y п 0 п-1 |
|
П-2 |
|
(-1) |
О
/
Л =
|
ПУп-Г 4° О |
|
И)1 |
|
О |
|
О |
|
Ч1 ПУп О 0 |
|
О |
|
(-■У |
|
О |
/
Особенный интерес представляют матричные формы для малых значений п. Для многоугольника из четырех точек (п = 3) кривая Безье имеет вид
|
Be B & |
Р(*) = [(1-03 3/(1 — tf 3t2(l-t) ;3j
|
Во Bi Щ, |
Группируя коэффициенты, получим
|
P(t) = [l* ПГ |
-1 3 -3
3-6 3 -3 3 О 1 О О
|
= 4), |
Аналогично, кривая Безье четвертого порядка (г? многоугольником из пяти точек:
|
"-1 |
-4 |
6 |
-4 |
1" |
‘Во |
|
|
-4 |
12 |
-12 |
4 |
0 |
Bl |
|
|
6 |
-12 |
6 |
0 |
0 |
Fh |
|
|
-4 |
4 |
0 |
0 |
0 |
В* |
|
|
1 |
0 |
0 |
0 |
0 |
В* |