Изображение и преобразование точек
|
У |
|
В трехмерном. Матрица- |
Изображение точек. Точка представляется на плоскости двумя своими координатами, которые определяются как элементы матрицы размером 1×2 [х у]. В трехмерном пространстве используется матрица размером 1×3 [х у Z].
Иначе говоря, точка может задаваться в виде вектор-столбца
В двумерном пространстве или в виде
строка или матрица-столбец с координатами точки часто называются координатным вектором.
Данное множество координат точки хранится в компьютере в виде матрицы или массива чисел. Положением точек можно управлять путем манипулирования соответствующей матрицей. Линии, соединяющие точки, формируют отрезки, кривые и картинки.
Преобразование точек на плоскости. Рассмотрим результаты умножения матрицы Р= [х у], содержащей координаты точки Р> на мат-
А B
|
Размером 2×2: |
|
С А |
Рицу общего преобразования Т
|
А Ь с D |
|
РТ = [х- у] |
— [(ял — + су) (Ьх + Dy)] = [х * у*].
Данная запись означает, что исходные координаты точки х и у Преобразуются в л4* и у*, где л* = ах + су у* = Bx+ Dy.
Представляют интерес значения у* — координаты результирующей, преобразованной точки Р.
Рассмотрим некоторые специальные случаи.
При A— D= 1 и с= Ъ-0 преобразование сведется к единичной матрице
1уГ = [х у]
О 1
И координаты точки Ростанутся неизменными. Как и следовало ожидать, в линейной алгебре умножение на единичную матрицу эквива лен гно умножению на единицу в обычной алгебре. В случае d=, b = С= О
|
РТ = [х у] |
А О
= [ах у] =[**/],
О 1
Где х* — ах- результат масштабирования координаты х. Рассмотрим другой случай: Ь= с = 0, т. е.
А О"
1>Т = [х у]
О D
Данное преобразование вызывает изменение обеих координат х и у вектора Р.
Если аФ D, то координаты масштабируются различным образом. При а= D> 1 происходит растяжение вектора Рили масштабирование координат. Если 0<«=Й?<1,То имеет место сжатие.
Если значение а или dотрицательное, то вектор отражается относительно координатных осей или относительно плоскости. Чтобы убедиться в этом, возьмем 6= с = О, D= 1 и а= 1, тогда
У] о =[-* ?]=[**Я.
И в результате получаем симметричное отражение относительно оси у.
Если Ь = с~ 0, а — 1, D = -1, то выполняется симметричное отражение относительно оси х. Если Ь= с= 0, а = D< 0, то происходит отражение относительно начала координат. Заметим, что обе операции отражения и масштабирование зависят только от диагональных членов матрицы преобразования.
|
Г*
Рис. 6.22. Поворот точки Р относительно начала координат |
|
Х |
Рассмотрим теперь случай с недиагональными членами. Возьмем сначала значения я=й?=1,с=0, тогда
Т = у] Q J =[х(Ьх + у)] = [х*у*.
Заметим, что координата х точки Р осталась неизменной, тогда как координата у* линейно зависит от исходных координат. Данное преобразование называется сдвигом. Аналогично в случае, когда а = D= 1, Ь= 0, преобразование к сдвигу пропорционально координате у. Таким образом, видно, что недиагональные члены матрицы преобразования создают эффект сдвига координат вектора точки Р.
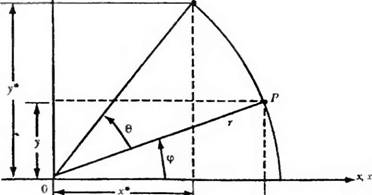
Поворот точки вокруг начала координат. Рассмотрим вектор положения гот начала координат до точки Р (рис. 6.22). Обозначим г— длину вектора, а <р — угол между вектором и осыо х.
Вектор положения поворачивается вокруг начала координат на угол в и попадает в положение вектора т*, а точка Р — в положение точки Р*. Записав векторы положений Ри Р получаем
Р= [х у] = [rcosG rsinG]
И
Г* = [х* У*] = [rcos(<p + 0) rsin(<p + G)], Используя формулу косинуса суммы углов, перепишем выражение для Г* как
Р* = [х* у*] = [r(cos(p cosG-sincp sinG) r(cos<p sinB -sintp cosG)]. Используя определения хи у, можно переписать 7** как
Р* = [jc* у*] = [xcosQ — у sinG xsinG +ycos0]. Таким образом, преобразованная точка имеет координаты
Х* = arcosG — у sin6; У* = х sinG + у cosG
Или в матричном виде
CosO sinG Х* = ХТ=[х* у*] = [ху] .
-smG cosG
Итак, преобразование поворота точки вокру1 начала координат на произвольный угол G задается матрицей
|
T = |
|
CosG |
-sinG |
|
|
SinG |
CosG |
|
= Т |
Cos6 sinG — sinG cosG
Повороты считаются положительными, если они осуществляются против часовой стрелки относительно точки вращения.
Предположим, что требуется возвратить точку Р* в точку Р, т. е. выполнить обратное преобразование — поворот г на угол G по часовой стрелке. Матрица для выполнения необходимого преобразования имеет вид обратной матрицы 7м, равной транспонированной матрице 7Т:
|
Г |
Cos(-G) sin(-G)
T~l =
-sin(-G) cos(-G)
Так как cos(-G) = cosG и sin(-G) = — sinG.
Однородные координаты. Во многих случаях при геометрических преобразованиях возникает необходимость изменять положение начала координат, т. е. преобразовывать каждую точку плоскости. Этого можно достичь путем перемещения точки начала координат или любой другой точки на плоскости:
Х* = ах + су + т У* = Bx+ Dy + п.
К сожалению, нельзя ввести константы перемещения ти пнача ла координат в (2х2)-матрицу преобразования, так как это не пространство.
Данное затруднение можно преодолеть, используя однородные координаты. Однородные координаты неоднородного координатного вектора f * у] представляют собой тройку 1*4′ И, где х= дс’/А. у-у’/А. а /г— некоторое вещественное число. Заметим, что случай h = 0 является особым. Всегда существует один набор однородных координат вида [х у 1]. Мы выбрали эту форму, чтобы представить координатный вектор [* у] на физическои плоскости ху. Все остальные однородные координаты представляются в виде f/wc hy h Данные координаты не сохраняют однозначности, например все следующие координаты [6 4 2J, [12 8 4], [3 2 1] представляют физическую точку (3, 2).
|
Т — |
Матрица преобразования для однородных координат имеет размер 3×3. В частности,
A B О с D О Та п 1
Где действие элементов а, Ь, с и г/верхней части (2х2)-матрицы точно соответст вует действиям, рассмотренным ранее. Элементы M и 72 являются величинами перемещения в направлениях х и у соответственно. Полная трехмерная матрица преобразования имеет вид
|
= [х+ M у + п, |
Отметим, что каждая точка плоскости и даже начало координат х = у = 0 теперь могут быть преобразованы.
Поворот вокруг произвольной точки. Ранее мы рассматривали вращение, совершаемое вокруг начата координат Однородные координаты предусматривают механизм выполнения поворотов вокруг точек, отличных от начала координат. В общем случае поворот вокруг произвольной точки может быть реализован посредством ее перемещения в начало координат, выполнения требуемого поворота и последующего перемещения результата обратно в исходный цен тр вращения. Таким образом, поворот вектора [х у 1] вокруг точки (га, п) на произвольный угол можно осуществить в виде
|
1 |
О о- |
COS0 |
SmO |
0 |
"1 |
0 |
0 |
|
|
Гх* у* 1] = [х у 1] |
0 |
1 0 |
-sinG |
CosG |
0 |
0 |
1 |
0 |
|
-VI |
-п 1 |
0 |
0 |
1 |
771 |
П |
1 |
Для сокращения будем записывать cosG как с, a sinG как S. Выполняя действия над двумя внутренними матрицами, можно записать
С S О
-5 С О
—т(с — 1)н Tls -?z(c-l)-7?is 1
Отражение относительно произвольной прямой О i ражение относительно произвольной прямой можно осуществить, воспользовавшись процедурой, аналогичной вращению вокруг произвольной точки. при этом выполняются следующие действия:
Перемещение линии и объекта таким образом, чтобы линия прошла через начало координат;
Поворот линии и объекта вокруг точки начала координат до со впадения с одной из координатных осей; отражение относительно координатной оси; обратный поворот вокруг начала координат; перемещение в исходное положение.
В матричном виде данное преобразование имеет предст авление
Ж= Т RR‘ R 1 Г
|
[л:* у* 1J = [л; у 1] |
Где Т’ — матрица перемещения; R— матрица поворота вокруг начальной координаты: R‘ — матрица отражения.
Геометрическая интерпретация однородных координат. Матрицу преобразования размером 3×3 для двумерных однородных координат можно разбить на четыре части:
|
А |
B |
Р |
|
|
7 = |
С |
D |
Ч |
|
M |
П |
S |
Напомним, что а. Ь. си D — коэффициенты масштабирования, вращения, отражения и сдвига соответственно. Элементы M и п задают перемещение. Установим величины р и Q не равными 0. Какой эффект
мы получим^ В данном случае полезно рассмотреть геометрическую интерпретацию.
При P=Q= 0 и 5=1 однородные координаты преобразованных векторов всегда равны H— 1.1ёометрически данный результат интерпретируется как ограничение преобразования физической плоскостью H= 1.
Для иллюстрации эффекта преобразования при р и q, отличных от нуля, рассмотрим следующее выражение:
|
1 0 р О 1 Q О 0 1 |
|
[х у 1] |
|
(6.114) |
[х у (px + qy+l)].
Здесь h~ Рх+ qy+ 1. Преобразованный координатный вектор, выраженный в однородных координатах, лежит теперь в трехмерном пространстве, определенном как А = рх+ qy + 1.
Однако представляют интерес результаты, принадлежащие физической плоскости с H = 1, которые можно получить путем геометрического проецирования точки с плоскости h-ф 1 обратно на плоскость H = 1 с использованием для этого проецирующих лучей, проходящих через начало координат.
Нормализуя выражение (6.114) делением однородных координат на величину H, получаем
[х* у* 1] = [х//г y/h 1J = [X/(px+qy+l) y/{px+qy+) 1], где X* = x/(px+ qy + 1); у* =y/(px+ qy+ 1).
Оставшийся элемент (ЗхЗ)-матрицы преобразования соответствует пропорциональному масштабированию, при котором все компоненты вектора изменяются пропорционально. Покажем это, рассмотрев следующее преобразование:
|
О О |
|
1 О О |
|
0 1 о |
|
= [х у s]. |
|
[х у 1] |
После нормализации получим х* = х/s и у* = y/s. Преобразование [х у ]Т= [х/S y/s 1 ] является равномерным масштабированием координатного вектора. Если S> 1, то происходит растяжение, а если л < 1 — сжатие
Преобразование точек в пространстве. Способность визуализировать или изображать пространственный объект является основой для понимания формы этого объекта. Кроме того, во многих случаях
Важна способность вращать, переносить и строить виды проекции объекта. Все это легко демонстрируется на примере нашего знакомства с относительно сложным незнакомым объектом. Чтобы понять его форму, мы тут же начинаем вращать объект, отодвигать на расстояние вытянутой руки, передвигать вверх и вниз, вперед и назад и т. д. Чтобы сделать то же самое с помощью компьютера, мы должны распространить наш предшествующий двумерный анализ на три измерения. Основываясь на полученном опыте, мы вводим однородные координаты. Таким образом, точка в трехмерном пространстве [х у Z] представляется четырехмерным вектором
[х’ у’ z* h] = [х у z 1] Г, Где Тявляется матрицей преобразования.
Как и ранее, преобразование из однородных координат в обычные задается формулой
[х* у* Z* H] = [х /H y/h z/h 1] .
Обобщенную матрицу преобразования размерности 4×4 для трехмерных однородных координат можно представить в следующем виде:
A b С р d Е f q g Г j Г ‘ I m П s
Матрицу преобразования 4×4 можно разделить на четыре отдельные части:
|
А |
B |
С |
P |
|
D |
E |
F |
Q |
|
G |
Г |
J |
R |
|
I |
M |
N |
S |
Верхняя левая (ЗхЗ)-подматрица задает линейное преобразование в форме масштабирования, сдвига, отражения и вращения. Левая нижняя (1×3)-подматрица задает перемещение, а правая верхняя (3 xl )-подматрица — перспективное преобразование. Последняя правая нижняя (1х1)-подматрица задает общее масштабирование.
Общее преобразование, полученное после применения этой (4×4)- матрицы к однородному вектору и вычисления обычных координат,
называется билинейным преобразованием. Б общем случае данное преобразование осуществляет комбинацию сдвига, локального масштабирования, вращения, отражения, перемещения, перспективного преобразования и общего масштабирования.
Трехмерное масштабирование. Диагональные элементы (4×4)- матрицы обобщенного преобразования задают локальное и общее масштабирование. Дпя иллюстрации этого рассмотрим преобразование, которое показывает действие локального масштабирования:
TOC o "1-3" h z А ООО
О fl О О
|
РТ=[х у Z 1] |
|
= [ах еу Jz 1]=[х* у* Z* 1]. |
0 0 0 5
Общее масштабирование можно осуществить, воспользовавшись четвертым диагональным элементом т е.
|
РТ=[х у Z 1] |
|
= |х’ у’ z‘ 5] |
Обычные или физические координаты имеют вид [х* у* Z* 1]=[х’/5 у /5 z‘/S 1]. ‘рсхмерные сдвиги. Недиагональные элементы в верхней левой (ЗхЗ)-подматрице обобщенной матрицы преобразования размером 4×4 задают сдвиг и в трех измерениях, т. е.
|
IT = [Х У z I] |
= [Х + dy + gz bx + y + iz r, x + Fy + z 1].
Трехмерное вращение Прежде чем переходить к трехмерному вращению вокруг произвольной оси, рассмотрим вращение вокруг каждой из координатных осей. При вращении вокруг оси хостаются неизменными х-координаты координатного вектора Фактически вращение происходит в плоскостях, перпендикулярных оси х. Аналогичным образом вращение вокруг осей у и z происходит в плоскостях, перпендикулярных осям у и ZСоответственно. Преобразование
Координатного вектора в каждой из этих плоскостей задается матрицей двумерного вращения. Эта матрица и неизменность координаты л: при вращении вокруг оси х позволяют записать (4х4)-иреобразова — ние однородных координат при повороте на угол а в виде
TOC o "1-3" h z 10 0 0
0 cosa sina 0
0 — sina cosa 0
Вращение считается положительным в смысле правила правой руки, т. е. ио часовой стрелке, если смотреть из начала координат в положительном направлении.
|
Ч- |
Аналогично матрица преобразования для вращения вокруг оси у На угол (3 имеет вид
Cosj3 sin(5 0 0"
-sinj3 cosP 0 0
|
Т = ‘а |
0 0 10
0 0 0 1
При вращении вокруг оси у на угол у преобразование имеет вид
|
Cosy 0 0 1 Siny 0 0 0 |
|
-siny 0 0 0 Cosy 0 0 1 |
|
7: = |
При комбинированном повороте последовательно относительно осей х, у и z соответственно на углы a, Р и у матрица преобразования получается путем последовательного перемножения матриц Та, 7р и Т
A Р у
Трехмерное отражение. В трехмерном пространстве отражение происходит относительно плоскости
При отражении относительно плоскости ху изменяются только значения z-координаты координатного вектора объекта. Таким образом, матрицы преобразования 7^, и 7^ для отражения относительно плоскостей ry, Yz и Xz равны
TOC o "1-3" h z -1 о о о
|
О о о о -1 о О 1 |
|
1 О о О |
|
1 О О 1 О о О о |
|
; Ъ = |
|
; Туг |
|
Т Ху |
ООО
-1 о о О 1 о О о 1
Пространственный перенос. Матрица пространственного переноса имеет вид
|
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
/ |
7П |
П |
1 |
Перемещенные однородные координаты получаются с помощью преобразования
|
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
1 |
771 |
71 |
1 |
|
[x’y, z’/i]=/T = [x У 2 1] |
Выполнив умножение, получим
[х’ у z h] = [(x+l) (y+m) (z+n) 1].
Из этого следует, что преобразованные физические координаты равны
X* = X + 1 у*=у + 7П 2* = 2 + П.
Композиции преобразований. Последовательные преобразования могут быть скомбинированы или объединены в одно (4х4)-преобразова — ние, дающее тот же самый результат. Так как перемножение матриц является некоммутативной (неперестановочной) операцией (АВ * ВА), то важен порядок ее выполнения. Правильный порядок определяется положением конкретной матрицы преобразования относительно матрицы координатного вектора. Матрица, ближайшая к матрице координатного вектора, задает первое преобразование, а последняя — последнее преобразование. Математически это можно записать следующим образом:
РТ= РТТ…Т,
12 71 *
|
7 = |
Где Т= 7jТ2… Тп — произвольная матрица маштабирования, сдвига, вращения, отражения, переноса, перспективного преобразования и проецирования.
Так как перспективные преобразования искажают геометрические объекты, а преобразования проецирования приводят к потере информации, то в случае наличия этих матриц они должны быть расположены соответственно предпоследней и последней по порядку.