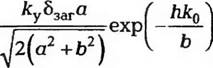Негативное формование (формование в матрице) обеспечивает получение тары, наружная поверхность которой воспроизволит фор­му и тиснение внутренней поверхности матрицы

Принципиальная схема метода показана на рис 5.11. Лист или пленка 3 раскраивается по размерам и закрепляется в раме 4 На закрепление листа расходуется время 1з1 Далее подводится наг рева­тель 5, и заг отовка нагревается в течение определенного времени до заданной температуры, после чего он отодвигается и подвигается камера 6 или вакуумный стол 9 Стол плотно прижат к npoFладкам- уплотнениям рамы 4 или к прокладкам в Либо подается давление (о), либо подв< >дится вакуум (я), которые, деформируя лист, плотно при­жимают его к поверхности формы 2

Рас. 5.11 Схема негативного пневматического и вакуумного формования тары: о — подогрев листа; б — пневматическое формование, в — вакуумное формование

Воздух, находящийся в полости формы (б), при формовании выхо­дит через каналы Эта же форма может быть использована и для схемы (в). Время, затрачиваемое на формование, равно t. После это­го внешним потоком холодного воздуха вновь отформованная тара 7 обдувается в формах, охлаждается и приобретает формоустойчивосгь. Время охлаждения — T . Рама снимается, а тара вместе с остатками

* ОХЛ

Заготовки по периметру выталкивается избыточным давлением воз­духа, подаваемым через каналы 1, либо удаляется ручным способом. На это тратится время разгрузки t.

При анализе параметров процесса негативного формования тары из листовых полимеров вначале рассмотрим формование простей­ших осесимметричных изделий в виде кругового усеченного конуса (рис. 5.12). С целью классификации подобных изделий по глубине вытяжки воспользуемся понятием коэффициента геометрии формы [69], который определится следующим образом:

L(l + cosa) Ф= 2R ~

Где L—длина образующей; a — угол наклона образующей; R — ради­ус большего основания усеченного кругового конуса.

O—Db

Рис. 5.12. Расчетная схема негативного формования при Ф > 1

Процесс оформления тары негативным методом можно разделить на несколько этапов: свободное формование; оформление боковых стенок тары; оформление днища тары; совместное оформление бо­ковых стенок и днища тары.

В зависимости от коэффициента геометрии формы эти стадии могут проходить в различной последовательности. Если формуемая тара имеет Ф > 1 f то ее формование состоит из свободного формова­ния заготовки; формования боковой поверхности; совместного фор­мования боковой поверхности и днища.

Если конфигурация тары характеризуется Ф < 1, то ее формова­ние состоит из свободного формования заготовки; формования дни­ща; совместного формования боковой поверхности и днища.

При Ф = 1 формование тары может рассматриваться как част­ный случай любого из названных выше процессов и состоит из двух стадий: свобод ного формования заготовки; совместного формования боковой поверхности и днища.

Проанализируем вариант при Ф > 1 [69]. На первом этапе проис­ходит процесс, аналогичный свободному формованию в круглой прой­ме; заготовка принимает форму тонкостенной оболочки с радиусом кривизны R0 = R/Sina.

Пл< щадь поверхности этой оболочки определим с помощью урав­нений (5 22), (5.23), (5 26):

Y =sma,

B0=-kymb^r, (5.36)

|l-Vl-sin2a |

5 =

Sin2 a

^ — ~ CLi (1-cosa)

S = S 2NR = — — —————- ; (532)

Sm a

Тилщину стенки оболочки определим из следующих соображе­ний. Объем материала, находящийся над полостью матрицы, до на­чала формования равен

V3ar=nR%„. (5.33)

Объем стенок оболочки в кон це свободного этапа ее оформления будет

2KR бг. П-cosa)

Щ——— 1. (5 34)

Sm a

Так как весь объем материала заготовки, расположенный над по лостью матрицы, идет на образование оболочки то V = V откуда искомая толщина стенки равна

(5.35)

Где т = sin u/(l — cosa) — коэффициент, определяемый конуснос­тью будущей тары.

Практически же величина 50 будет несколько больше, так как ра — зогретый материа л частично ут ягивается в полость матрицы из про­странства, ограниченного отверстием зажимного устройства, но не находящегося над полостью матрицы, а также из-под самой зажим­ной рамы Поэтому выражение (5.35) следует уточнить, введя попра­вочный коэффш щент:

2

Где ку — коэффициент утяжки материала.

На втором этапе формования оболочка, которая до этою не каса­лась матрицы, втягиваясь внутрь формы, образует коническую часть с длинои образующей Dl, соприкасающуюся с поверхностью матри­цы, и сегментную оболочку с толщинои стенки < 50. В дальнейшем эта оболочка также втягивается, образуя новый конический участок и новую оболочку с толщиной стенки?>2 < .’ )тот процесс повторяет­ся до тех пор, пока последняя оболочка с толщинои стенки 5 не со­прикоснется с дном матри цы.

Предположим, что полимер, который в процессе формования со­прикасается со стенкой, вследствие почти мгновенного охлаждения образует на своей наружной поверхности тонкую твердую корку, температура которой значительно ниже температуры формования данного поли мера. Это происходит в результате того, что температу­ра матрицы редко превышает 220 — 240 К Образовавшаяся корка препятствует дальнейшей вытяжке материала из элементарного ко­нуса.

Здесь надо оговориться, что данное предположение может быть справедливо лишь при формовании изделий из резиновых смесей, что, вероятно, объясняется большим коэффициентом треиия сырой резины по поверхности формующего инструмента.

Рассмотрим процесс формования, когда вытяжка происходит на глубине, соответствуя щей длине образующей I — В этот момент фор­муемая заготовка представляет собой сочетание двух тел: конуса с

Р*1Диусом основания R и объемом стенки V и шарового сегмента

Радиусом rz и объемом стенки V

В следующее мгновение дл ина конической части увеличивается Hd Dl, и объем ее стенки станов ится равным

(5 37)

Сегментная часть оболочки утонится на величину dfi, а объем ее стенки станет равным

(5.38)

Так как объем формуемого материала в течение всего процесса остается неизменным, то из выражений (5.37) и (5 38) следует, что

DVY«=dV’:er. (5 39)

Элементарное изменение объема стенок оболочки шарового сег­мента может быть выражено следующим образом:

DVier = C°S%(25cosarti + R}db).

Sin ft

При ф( (рмовании тары из терм< )Нластов образование поверх ност — ной корки на конической части может полностью прекращать вы­тяжку из части материала, соприкоснувшейся со стенкой или толь­ко уменьшить ее.

(5.41)

Кроме того, можно предположить, что процесс теплообмена осу­ществляется не только в направлении границы между конусной и сегментной оболочками, охлаждая при этом каку ю-то часть матери­ала, находившуюся в этот момент в сегментной оболочке и не сопри­коснувшуюся со стенками матрицы. Поэтому в выражение для оп­ределения элементарного объема стенок конической части вводится коэффициент кр

DV^ = HcQiirfidl.

При этом возможны три слу чая-

Ес:ли KQ< 1, то это означает, что часть материала уносится с кони­ческого участка;

Если к = 0, то материал, соприкоснувшись с матрицей, больше не вытягивается;

Если к > 1, то охлаждается некоторое к(>личество материала, на­ходящегося в сешет нои части оболочки.

Последний вариант нежелателен, так как привс >дит к браку При охлаждении материала, находящегося в пограничной части сегмент­ной оболочки, может образоваться некое подобие обруча, более жес­ткого. чем весь остальной материал И если давление формования недостаточно высоко, такой обруч не будет плотно приформован к стенке матрицы. Приформуетсялишь находящийся ниже этого об­руча материал, температура которого не успела опуститься ниже м инимал ьно допу стимой температуры формования. На таре образу­ется кольцевой гофр Аналогичный процесс проходит по всей высо­те формуемой тары.

(5.40)

При формовании изделий из резиновых смесей KQ< 1. Подставив уравнения (5 40) и (5.41) в (5 39), получим

D6

Dl

(5,42)

K0 — 2cosa

K-Zcosa

Sm a 1-cosa

Так как ь п роцессе форм* жания длина образующей меняется от О до I, а толщина сегментной оболочки от до 8, то, проинтегрировав уравнение (5.42) в этих пределах, получим

( 2 sm a

Dl

К0 -2cosa

(5.43)

1-cosa

D8

=-j:

0R-lcOsa 6q 5

Или

I-	(0
—	Cosa
	UJ

(V-2)ln

= ln(5/50),

(544)

Где f — л?/cos a.

-2+kJ

Б)

(5.45)

Cosa

-2+V

I

Потенцируя (5 44), получим

5 = 50

Или, учитывая уравнение (5.36).

1-1 — cosa R)

(5 46)

8 = 0,5ткудзаг

1

Частным случаем формования конических изделий является из — I отовление тары в виде круговых цилиндров Положим в уравнении (5 44) a = 90, так как в это м случ ае Koi гическая матрш (а превращает­ся в цилиндрическую Угод дополняющий 90°, X — 90 — а-при a = 90 X -» 0. Тогда левая часть уравнения (5.44) примет вид

F cos2 X

1-smX

Г

= lim

1

Ьш Х^о

К0 -2sinX

In

SmX 2Х

У

-2^

(1-Х)

X R

Х-»о

1-—SmX R

= -/c0l. 0 R

Таким образом, приХ-»0,т. e при a = 0, выражение (5 44) приоб­ретает вид

-к

Но при а -» О I — H (H — координата по высоте цилиндрического изделия), поэтому

Ло

После преобразования получаем уравнение ддя цилиндрической тары:

R Г

‘ мВ

6 = ехр

Ь0=0,5куЬзаг. (5.481

(5.47)

Леси учесть, что для цилиндрического изделия т = 1, то уравне­

Ние (5.36) приобретает вил

М R

(5.49)

Б = 0,5/cvS3ar ехр|

Для определения ко э ффициентов киик используется следующая полузмпирическая методика. Логарифмируем уравнение (5,46) и получаем ура внение прямой:

(

. I

-lnfi

У^заг»

-2 + V

1— — cosa R

-2 + V

Где 1/(-2ч Ао/) —тангенс угла наклона прямой;

[l/(-2 + Kqf) In 0,5 Mkyb^ —отрезок, отсекаемый данной прямой на оси ординат.

Таким образом, нанеся экспериментальные точки и объединив их прямой в координатах In5-lr 1 -(i/J?)cosa]f можно вычислить

Л

1

1

1п0,5лтк.6

In

Коэффициент I г и средний для данного процесса коэффициент к, На рис. 5.13 в качестве примера представлено изменение по высо­те толшины изделия в виде усеченного конуса, отформованного из листа ударопрочного полистирола толщиной 1,7 мм, в логарифми­ческих координатах. Формование проводилось при температуре заготовки 403 К

0,1 0 2

Рис 5-13. Изменение толщины стенки по высоте изделия при температуре формы 29.1 (J) и 343 К (2)

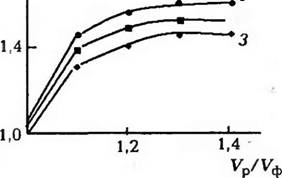
Изменение коэффициента к в зависимости от отношения объема части заготовки, ограниченной отверстием зажимнои рамы V, к объему части заготовки, находящейся непосредственно над матри­цей V, при температуре листовой заготогки из ударопрочного поли стирола 388 и 403 К показано на рис 5.14. С увелгпением отношения Vp/Уф коэффициент А:уасим] пготически приближается к определен­ному значению. Это связано с тем, что утяжка материала происходит в первую очередь из частей заготовки, ближе всего расположенных

18

«2

Рис. 5.14 Зависи чость коэффицие! Гга ку От отношения V /V при температуре листовой заготовки. К: 1 — 388; 2 — 403, 3 — 418

К матрице. Поэтому при д< >статочпо большом соот ношении V’ ‘V ко­эффициент & перестанет увеличиваться.

Коэффициент к. не зависит от температуры матрицы, а темпера­тура листовой заготовки сказывается на нем лишь в том случае, ког­да она высока настолько, что ис. т успевает прогреться под зажим­ной рамой Однако это увеличение столь незначительно, что им вполне можно п ренебречь.

Второй этап оформления тары при Ф > 1 заканчивается з тот мо­мент, когда сегментная оболочка соприкоснется с днишем мат рицы. Начинается третий этап — совместное оформление боковой поверх­ности и днища тары. Характер деформации материала заготовки на этом этапе чрезвычайно близок к процессу формоизменения заго­товки при формовании изделий с Ф < 1. Учитывая это обстоятель­ство. опустим описание третьего этапа негативного формования тары с Ф > 1, имея при этом в виду, что приведенный ниже анализ нега — тивного формования тары с Ф < 1 является практически и анализом третьего этапа формования тары с Ф > 1.

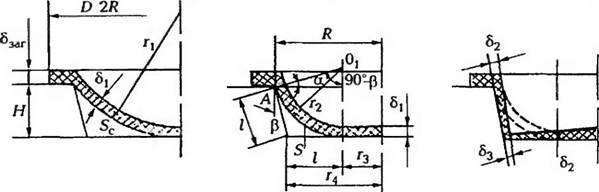
Условно разделим процесс формования таких типов тары с Ф < 1 на три этапа: образование сферического сегмента высотой Н (рис. 5 15, а), формование участка днища с радиусомг3 (рис. 5.15, б] и q. op мование утла изделия (рис. 5.15, в). При описании процесса формо­вания тары сделаем два допущения. 1) объем материала при формо — вании остается постоянным; 2) зависимость толщины стенки тары по высоте принимаем линейной.

В О

Б

А

Лис 5 15 Расчетная схема негативного термоформования. листовых полимеров при Ф < 1: а —- первый этап ф< »рмовач ия б — второй этап; В — окончательное оформление изделия

Рассмотрим первую стадию формования. Под действием разно — с ги д< 1нлени й I [ад заготовкой и под ней происходит ее свободное фор­
мование с образованием сферического сегмента, который к моменту окончания первой стадии имеет высоту Ни радиус г

Первоначальный объем формуемой заготовки V определим из (5.33).

Объем заготовки к моменту окончания первой стадии будет равен

V, = = 2щНЬ19 (5.50)

H2+R2 где Г| = .

2 И

Приравняв на основании первого принятого нами допущения (5.33) и (5 50), получим среднее значение толщины стенки сферичес­кого сегмента

1 б

‘ 1 + (Н,/Я) г или обозначив Н/R = К и учитывая коэффициент ку:

К

^^-Ът^заг — (5.51)

1 т П

Вторая стадия на чинается в тот момент, когда заготовка коснется дна формы. Она характеризуется оформлением днища тары. При этом происходит постепенное уменьшение толщины заготовки, и в конце второй стадии на расстоянии ri от оси тары толщина днища уменьшается до величины 52.

Для определения значения 52 приравниваем объем заготовки в конце первой стадии к сумме объемов материала, находящегося на участке днища с радиусом г3, и материала, составляющего часть то — ровой оболочки с радиусом г2:

\=V2+V^ (5 52)

V2 найдем как сумму объемов цилиндра и конуса, учтя при этом ко­эффициент^.

V2=^7(8,+2S2), (5.53)

Объем части торовой оболочки V определится как

И

V,^S2JydS, л

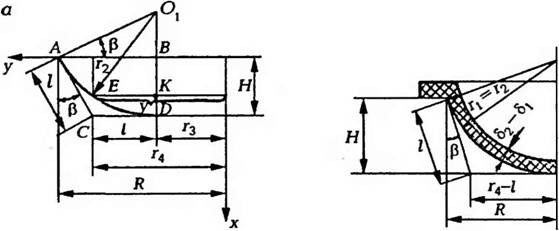
Где А и D — крайние значения параметра, через который выражают­ся координаты; хи у— координаты точек, принадлежащих дуге AD.

DS = yJ+(y’fdx.

Рис. 5.16. Расчетная схема к определению величины дифференциала дуги DS (а); расчетная схема для случая гА = 1 (б)

Из геометрических соображений (рис. 5.16) получаем

У —

DS

У = r3+^r2-(r2sinp + x)2,

Откуда

R2sinp + x

Л/г22 -(rsinP + x)"

Тогда

Г dx "VГ22 ~(r2sinp + х)2

71

Г3 —Р +Н

(5.54)

= 2яб2 {ydS = 2Я62Г2 R

(5.55)

Подставив (5.33), (5.53) и (5.54) в (5.52) иучитывая (5.51), определяем

Выразив значения радиусов г2иг, через заданные нам геометри­ческие пара метры формы H/R = /сир. преобразуем уравнение (5.55).

У 341	" iC(l + smp) cosp	2
1+ К2 2 к0	K(l + smp)	2 6К2	1 +	Г 1 l + sinp"!	H
1 Cosp	1-sinp	KK cosp y

6,=

(5.56)

Для определения границ изменения полученного уравнения рас­смотрим случай, при котором (рис. 5 16, б) г = 1. Выразив H,R, К через длину образующей |, а коэффициенты А и к0 приняв равными едини­це, находим, что в этом случае

Я я я Hsinp Ь2=Ь I = 6заг ^ ■

Отсюда вндно, что при/ = 1 и, следовательно, при к = cosp/(1 + smfS) вторая стадия процесса отсутствует. Мин)*я вторую стадию, процесс переходит из первой в третью Таким образом, уравнение (5 56) спра­ведливо при условии 0<Л <со«р/(1 Ш Бпф).

На третьей стадии формования часть торообразной оболочки с радиусом г2, изменяющимся от И/{1 — smp) до 0, постепенно образу­ет днище и стенку тары К концу этой стадии оформляется угол меж­ду стенкой и днищем тары, толшину стенки в этом месте принимаем равной 6

Для определения величины 6, приравниваем объем части торооб­разной оболочки V к сумме объемов кольцевой части дна, ограни­ченной радиусами г3 и с4(У), и наклонной стенки V"5. При этом ис­пользуем наше второе допущение и будем считать, что уменьшение толщины днища от до 63 описывается уравнением прямой линии

V3=V4+V5. (5.57)

V;

Легко показать, что

V4 = ^[П (H + 2б3) — г2 (232 + 63) + г3г4 (52 — б3) |, (5.58) ПИ

(5.59)

3cosp

Подставим в (5.57) уравнения (5 54), (5.58), (5 59) и выразим г,, гу г, H.R через К ир

CosP l + 2sinp

К

-1

1-sinp 3cos0

63 = 52

CosP A(l + sinp)

I-sinP 1-sinp

J K( l + 5sinp) 6cosp

Или через i ол] цину за) отовки

62 =8,drMN,

(5 ъо)

Гдр

	З(1 + К2)-к0	" K(i + smP)	2
Ку	V / 0	Cosp

71

М =

1 L + sinJ ^К cosp

1 К( i + sinp) cusp

Б К

1 +

I — snip

2 к,

К	Cosp 1 + 2sinP>		Cosp iC(l+sinp)"	-1
	1-sinp 3cosp J	42 HJ	1-sinp 1-sinp

N

I

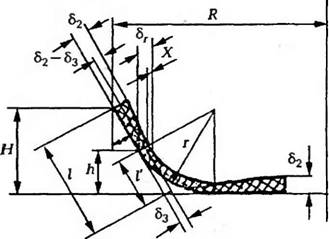
Как правило, между днищем тары и ее стенкой имеется радиус скругления г (рис. 5.17). В этом случае толщина стенки тары в месте скрутле] доя 6г может быть определена из следу* >гцего соотношения: Рис 5 17. Расчетная схема скругления в углу тары между днищем и боковыми стенками

K(l_+5sinp) 6cosp

Где X ~(62 — 63)Ц/1, Zj =r(l-sinP)/cosp, Z = H/cosp. Таким образом.

(5.61)

Ьг — Ъъ + (ПН)(Ъ2 — 53 )(1 — cosP). После подстановки (5 56) и (5.60) в (5.61) получим

=S3arM

(5.62)

Г

(l-N)(l-smp) + N

Н

При Р = 0, т. е. для тары, имеющеи ттилиндрическую форму, урав­нение (5.62) примет вид

(5.63)

Где

Ку з(1 + К2)	)-к0(-К)2
2 К 2к0{-К)2+6К	1+ П + 2(/К-)

Ш + Ъпк0([-к)-6

6-К

Очевидно, что приведенное выше описание негативного формо­вания простейших осесимметричныхтипов тары с геометрическим параметром Ф< 1 может быть полностью использовано для описания третьего, заключительного этапа ф< >рмования аналогтпньгх тнп< >в тары с Ф > 1. Для этого необходимо лишь учесть, что объем Vj в уравнении (5.52) есть не что иное, как объем свободно ф< >рмуемой сегментной части заготовки в конце второго этапа, т. е. в тот момент, когда эта часть заготовки прикасается к днищу матрицы лишь в одной точке.

Производство тары в виде кругового цилиндра и конуса является лишь частным случаем негативного формования. Большинство ти­пов тары имеет более сложную форму, что приводит соответственно и к более сложному описанию происходящих при этом процессов. Однако основные закономерности сохраня ются Так как всевозмож­ны х вариантов форм тары бесконечно много, проведем анализ пара­метров процесса формования на примэрелишь дву х конфигура! т: формы эллиптического цилиндра и формы параллелепипеда.

Понятие геометрического параметра Ф в том виде, в каком при­ведено в начале данного раздела, к изделиям, о которых будет идти речь в дальнейшем, неприменим. Его нужно несколько модифици­ровать В случае формования тары в виде эллиптического цилиндра или эллиптического конуса при определении геометрического па­раметра Ф’ значение радиуса большего основания усеченного кру­гового конуса R должно быть заменено значением малой полуоси боль­шого основания усеченного эллиптического конуса, А при формова­нии тары в виде параллелепипеда значение R заменяется значением половины малой стороны прямоугольника, лежащего в основании.

Итак, рассмотрим процесс негативного формования тары, имею­щей вид эллиптического цилиндра с плоским днищем Ф’ > 1. Здесь и в следующем примере рассмотрим лишь две первые стадии процес­са как наиболее характерные. При этом будем помнить, что наша основная задача в данном случае — показать, что при формовании тары более сложной формы основные закономерности процесса ос­таются те же, что и при формовании тары простейшей осес. иммет — ричной формы.

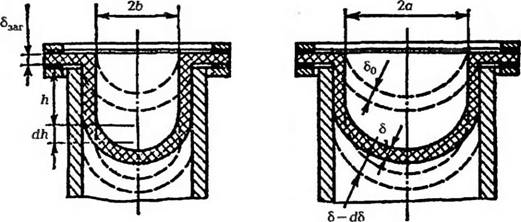
Учтем, что объем материала, составляющего на стадии свободно­го формования стенки полуэллиптической оболочки (рис. 5 18), ра­вен объему термопласта, наход ившегося непосредственно над поло­стью матрицы до момента начала формования. Приравняв эти два объема, можно определить среднюю толщину стенки свободной по­луэллиптической оболочки 50. Однако при этом следует учесть, что разогретый до высокоэластического состояния термопласт в процес-

Рис. 5.18. Расчетная схема негативного формования тары в виде эллиптического цилиндра при Ф > 1

Се формова ния частичнг»утягивается в полость матрицы из простран — ства, ограниченного отверстием зажимной рамы, но не находящего­ся над полостью матрицы

6л = к. ГЬ

(564)

У v3ar

-1-1

Ь arcsine

— н—-

(5.65)

А е

Где а и Ь — соответственно большая и малая полуоси эллипса; е — эксцент риситет — эллипса

Yja2-b:

£ =

А

На тл орой стадии форм» >вания при контакте термопласта с рабо­чими поверхностями матрицы стенки свободно формуемой полуэл­липтической оболочки утоняются, и часть термопласта расходуется на образование эллиптического цилиндра Элементарное изменение объема стенок образующейся цилиндрической части определяем выражением

DVy =4/c0of bdh,

Где Dh — элементарное изменение координаты и высоты изделия; E(7i/2,e) — полный эллиптический интеграл

(5 66)

Элементарное изменение объема стенок нолуэллит ическои обо­лочки равно

, B агспп^Л

DVl =nab — +——— (ifi.

[а г J

В процессе форм< даания объем термопласта остается постоянным. Поэтому, приравняв уравнения (5.65) и (5.66), разделив переменные и подставив с< ютветствующие пределы, интегри руем вновь получен­ное выражение и, заменяя значение 50 в соответствии с (5 64), полу­чаем

Ь arcsine 1

— +——— ехр

%

4М0Г

(56V)

5 — ^yS3ar

-й

Arcsine 1 J

А z )

Эту зависимость можно представить и в более простом, прибли­женном виде, однако в этом случае следует пользоваться упрощен-

Ными формулами для расчета длины периметра эллипса Р и поверх­ности полуэллипсоида вращения S:

(5.68)

Б

Расхождение результатов, вычисленных по формулам (5.67) и (5 .68), колеблется в пределах 6 — 8% в зависимости от соотношения величин полуосей эллипса, лежащего в основании тары. При а = B = R зави — симости (5 67) и (5.68) преобразуются в уравнение для изделия в фор­ме кругового цилиндра вида (5.49).

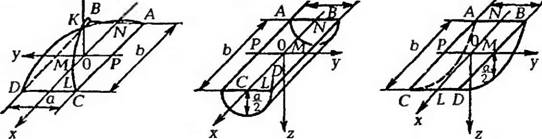
Теперь рассмотрим негативное формование тары, имеющей фор­му параллелс * грамма (Ф > 1) На первой стадии разог ретая листовая заготовка деформируется под действием разности давления и при­обретает вид вогнутой поверхности, границы которой имеют фирму прямоугольника, повторяющего геометрию верхних кромок форму­ющего иш трументи При этом, как и в предыдущих случаях, заготов­ка не входит в контакт с рабочей поверхностью формующего инст­румент а Если поперечное сечение рабочей полости формующего инструмента представляет собой прямоугольник а х Ь, причем а <br то можно сделать допущение, что сечение поверхности формуемой заготовки в плоскости Zox (рис. 5.19) будет представлять собой часть

Б

В

А

А

А

Рис. 5.19 Схема дя определения площади пове) >хности на гюрв< >й стадии негативного формования тары в виде параллелепипеда: а — свободная поверхность, б — круговой цилиндр, в — эллиптический цилиндр

(повернули на 180°) z 1

Дуги эллипса, сечение Zox— часть душ окружности. Если же а я Ь, То при сечении поверхности заготовки как в плоскости Zox, так и в плоскости Zoy получается часть дуги окружности.

Как и в предыдущих случаях, вторая стадия формования характе­ризуется процессом дальнейшего деформирования поверхности за­готовки Этот процесс сопровождается контактом термопласта с по­верхностью формующего инструмента.

Границей двух стадий является момент, когда касательная, про­веденная через точку Рили М к дуге ок ружности, получающейся при сечении поверхности в плоскости Zox, совпадает с плоскостью рабо­чей поверхности матрицы I Тосле этого формуемая заготовка войдет в контакт со стенками формующего инструмента.

Для определения пл< >щади поверхности форму емой заготовки на границе первой и второй стадии предположим, что данная повер­хность образована двумя цилиндрическими поверхностями: по­верхностью кругового цилиндра радиусом а/2 с образующими, па­раллельными оси х, и поверхностью эллиптического цилиндра с большой полуосью Ь/2, малой полуосью а/2 и образующими, па­раллельными оси у Линиями пересечения описанных цилиндри­ческих поверхностей будут яв.яться кривые BKCuAKD.

Таким образом, искомую площадь поверхности формуемой заго­товки можно представить как сумму площадей участков поверхнос­тей кругового и эллиптического иилиндров.

J (5 69)

Площадь участков эллиптического "илиндра

Ь,2*И>) (afbfx2

( о V (ь/а) ~[3]

1 1

Площадь участков кругового цилиндра

TOC o "1-3" h z У(Ь/а)а/2 / 2

Fk=4 ‘ J J1* , /М2 2*ХШ*- **»

О О V — У

Сложив площади, заменив переменные и произведя соответству­ющие преобразования, получим площадь искомой поверхности

Г .

^пов =2ab-b2

1 ~(a"b)2

1п|* + ^1-(<э’Ь)21 (5.71)

Анализируя вторую стадию формования, можно заметить, что в любой момент формуемая заготовка на этой стадии состоит как бы из
двух частей: из образующего участка боковых стенок изделия и сво­бодной поверхности, идентичной рассмотренной выше и отличаю­щейся от нее только толщиной, что характерно для всех ра ссмотрен — ных в этом разделе типов тары с Ф > 1.

Толщину термопласта, образующего начальную поверхность, можно определит]», исходя из следующих предпосылок:

А) объем термоплас та при деформации заготовки остается посто­янны м;

Б) площадь за готовки к моменту окончания первой стадии формо­вания F ;

Тв"

В) исходная площадь заготовки о Xb

Таким образом,

<? » с

&о=*Лаг —-• (5.72)

"поь

По мере pea лизации второй стадии фо{ >м< >вапия толщина свобод­ной поверхности убывает. Общии же объем формуемой заготовки остается постоянным. Это дает право при равнять элементарное из­менение объема материала, образующего боковые стенки изделия к элементарному изменению объема материала, находящегося в сво — бодноформуемои поверхносги, т. е.

2*о (а + B)Bdh = Fn0B (-ml (5 73)

Где Dh — элементарное изменение координаты по высоте изделия (рис 5 18)

Разделив переменные и имея в ьиду, чго при изменении коорди­наты по высоте изделия от нуля до текущего значения H значение толщины стенки изделия изменяется от 50 до текущего 8, получим уравнение для расчета изделия, имеющего форму параллелограмма:

(

8 = 8П ехр

(5.74)

2(a + h)h

И учитывая (5 72),

5 = icv83dr ——ехр

К0 -2(a + b)h F 1 пов

(5.75)

"пои

Итак, из приведенных примеров видно, что общий механизм фор­мования тары негати вным методом остается постоянн ым, вне зави­симости от конфигурации тары. Конфигурация накладывает отпе­чаток лиш ь на разнотолщипность тары на тех или иных ее участка»

Таким образом, недостатками тары, полученной методом нега­тивного формования. являются:

1) существенная разнотплщинностьтары при глубокой вытяжке, особенно в углах и местах переходов (при малой глубине изделия разница в толщине не сто ль значительна);

2) разной толщиной характеризуется дно тары с максимумом ь центре и минимумом в углах, а также боковые сто] 1ки с максимум ом в районе зажимной рамки и минимумам в углах;

3) точную геометрическую форму и размеры имеет внешняя по­верхность тары. Внутренняя поверхш >сть формируется с учетом ] >аз — нотолщинности стенок, поэтому внутренни]i объем гары имеет су­щественный разброс.

Производство тары из полимерных пленок и листов

Особенности механических свойсть полимеров в высокоэластическом состоянии

Интервал температур, в котором можно наблюдать высокоэлас­тические свойства полимеров, равен разности температур (Т — Т) Для сетчатых полимеров верхним пределом эластических свойств является температура начала термического разложения Т, так как из-за межцепных химических связей полимер течь не может и при высоких температурах начинает разлагаться, деструктироваться, не переходя в текучее состояние Эластические свойства целесообразно рассмотреть на […]

Производство мягкой потребительской тары на фасовочно-упаковочных автоматах термоформовочного типа

Термоформовочные автоматы позволяют упаковывать любые виды продукции с использованием всех возможных методов ее по­дачи в отформованную часть тары. 11ижняятермоформованная часть из однослойного или многослойного полимерного материала являет­ся жесткой или полужесткой. Верхняя крышка отличается гибкос­тью, минимальной жесткостью. Она выполнена, как правило, из мно­гослойного материала, поэтому обладает хорошими барьерными свойствами, способностью к сварке ил и склеиванию, пригодна […]

Контакт но-тепловая сварка

Контактно-тепловую сварку нагретым ин< трументом осуществ­ляют с односторонним или л, вусторонним нагревом (рис. 4.41). Рис. 4.41. Схема контактно-тепловой сварки с од] юсторонним (а) и двусторонним (6) нагревом: 1 — нагретый инструмент; 2 — прокладки; 3 — свариваемые материалы; 4—холодный инструмент, мгн — температура нагретого инструмента; t2 — температура внешней поверхности изделия; Т —температура свариваемых поверхностей; […]