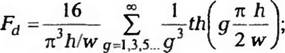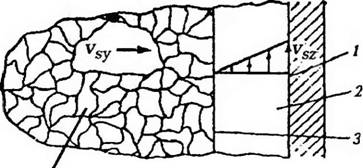
Математическое моделирование процесса экструзии пленок с раздувом осн< >вано на принятии ряда допущений, таких как пренеб­режение силами инерции, поверхностного натяжения, аэродинами­ческого сопротивления потоку. Форма рукавной заготовки опреде­ляется отношением линейной скорости экструзии пленки v? к сред­ней .линейной скорости эк ci рузии расплава на выходе из головки vQ, А также давлением раздува. При некоторых доггущениях коэффици­ент раздува K — D/D = йЛ0 и о гношение v FvQ определяют степень вы — тя жки полимера в заданных направлениях Описание процесса фор­мования изотропных пленок упрощается при допущении, что продоль­ная скорость от головки до. линии кристализапии (зона раздува L) v2 = const, а растягиваемый рукав имеет форму конуса. Тогда гради­ент скорости у = (vj — vjf/l, где у —скорость движения участка на расстоянии L от головки.

Объемные расход расплава О в различных сечениях рукава оп­ределяется соотношением

О = 2nr0h0v0 = 2r.RH, (3.1)

Где RQ — с реднии радиус кольцевого зазора головки, HQ — ширина коль­цевого зазора RnH— радиус рукава и его длина соот в< ягственно

Из приведенного соотношения следует, что для получения изот­ропных пленок рассматриваемым методом необходимо добиваться конической формы р^тсава и выполнения условия ht/H = к2.

В случае конической формы рукава его геометрические парамет­ры могут быIb определены из следующих Cooti юшений [8 47]

I = l+(B-l)f В=Щ

Го L ги

H L ВН LBH { ‘

Где величины г и H соответствуют переменным параметрам, опреде­ляемым на расстоянии Z от начала вытяжки, R — радиус рукава на высоте Н

Соотношения (3 1) и (3 2) позволяют рассчитать параметры изот­ропных пленок, например радпуг рукава R после раздува или (чтото же) ширину получаемого рукава, если известны характеристики го­ловки (г, г0) Возможно также определение номинальной толщины пленки

Длина зоны охлаждения рукавных пленок, как было показано выше определяется способом и интенсивностью охлаждения. При увеличении расхода охлаждающего воздуха или при понижении его температуры линия кристаллизации приближается к головке. Ох­лаждение пленки осуществляется вследствие отвода тепла за счет излучения Q и вынужденной конвекции Обычно Q составляет не более 10 — 20% от Of щего количества отводимого тепла Значение Q Определяютпз уравнения

Dqs=a(T-TL)dF, (3.3)

Где а — коэффи! щенттеплопередачи от пленки в охлаждающую сре­ду; Т— температура пленки, ITL — температура воздуха, используе­мого для охлаждения, F — площадь поверхности рукава в зоне ох­лаждения.

Значение а определяется по ск< >рости движения воздуха V :

A = 6,12VB0’78. (3.4)

Количество тепла, отводимого за время Dt от единицы площади пленочного рукава, определяется по формуле

DO = o.(T-TL)Fdt.

Большое значение имеют взаимосвязи основных параметров тех­нологического процесса экструзии пластических масс Для их изуче­ния создаются математические модели экструзии. Такие модели по­лучают совместным решением системы у равнений сохранения мас­сы, энергии, количества движения (в прил ожении к рассматриваемо­му процессу) с реологическими уравнениями состояния полимера.

(3.5)

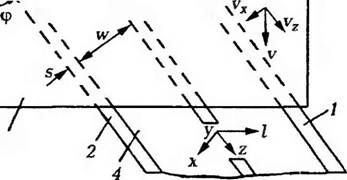
Если объемная производи гелыюсть экстру дера определяется ра­ботой зоны дозирования, то можно математически описать работу экструдера в этой зоне. Рассматривая так называемое «обращенное движение» (червяк неподвижен, а перемещается корпус) и пренеб­регая кривизной канала, м< >жно развернуть канал червяка на плос­кость и представить схематически процесс так, как он изображен на рис. 3 22. Если рассматривать установившееся течение и пренебречь массовыми силами инерции, то можно получить систему уравнении, описывающих движение жидкости, подчиняющейся степенному за­Кону вязкого течения при наличии теплообмена.

Е

W

\

3

ч ^

Рис 3.22. Развертка р. инто»юго канала червяка на плоскости 1 — стенка канала; 2 — гребень нарезки червяка, 3 — поверхность корпуса; 4 — канал

Для построения модели, допускающей аналитическое решение, делаются следующие допущения: 1) течение в направлении оси су­ществует только в непосредственной близости к стенкам канала; 2} размеры канала по всей длине постоянны, т. е. v и w не зависят от z; 3) температурный градиент в поперечном направлении пренебре-

Ось червяка

T

Ь

\ ~У

Жимо мал по сравнению с продольным. С учетом этих допущений уравнения равновесия в напряжениях сведутся к виду

ДРху дР

ZX

(3-6)

Ду dz Ду dz dz dz dy

Где P— гидростатическое давление в точке; ру—компоненты тензо­ра напряжений, действующего на элементарный объем.

Dp

Dp

Yz + Dp

Ар Дх

У* f Ф

ДР Dz

ЭР ду

Zy

Xz

Dz

Dv^ Ду

(3.7)

ДТ dvx

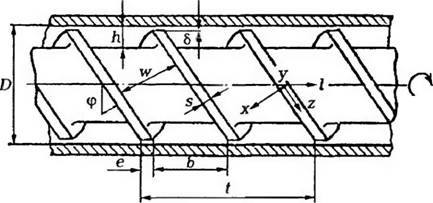
Где р — плотность экструдата; ср — удельная теплоемкость при по­стоянном давлении, v — проекции вектора скорости жидкости на соответствующие оси; ру — компоненты напряжении (первый ин­декс указывает ориентацию поверхности — направление нормали к площадке, к которой приложена сила; второй — направление, вдоль которого действует сила) (рис. 3.23). Рис. 3 23. Схема расположения координатных осей и обозначение геометрических параметров червяка С целью учета теплообмена с окружающей средой в уравнение теплового баланса вводят дополнительную характеристику процес­са — коэффициент политропичности к. Если все тепло, выделяюще­еся во время работы экструдера, отводится в окружающую среду, то К = 0 (изотермический режим) Если же все тепло, выделяющееся в результате внутреннего трения, остается в полимере, то к = 1 (адиа­батический режим). В реальных условиях имеют место промежуточ­ные режимы, когда помимо тепла от внутреннего трения расплав получает тепло от нагревателей. В этом случае 0 < к < 1.

При составлении энергетического баланса считают, что теплопе­редача вдоль оси канала пренебрежимо мала. Тогда

Используя коэффициент политропичности, уравнение (3.7) мож­но представить в виде

Орс^ DT — kdW — QdP,

Где О — объем расплава, проходящии в единицу времени через еди­ницу сечения канала; ср — колич ество тепла, необходимого для на­гревания единицы объема расплава на один градус; DW— работа вязкого трения на участке длиной Dz.

Основные дифференциальные уравнения изотермического ре­жима экструзии рассмотрены для случая экструзии «ньютоновской» жидкости и аномально-вязкой жидкости, подчиняющейся степенно­му закону течения.

Для построения математической модели используют приближен­ное решение, основанное на замене реального двухмерного тече­ния двумя независимыми одномерными течениями, С помощью эт< >и модели предпринимаете я поп ытка установить связь между дав­лением на выходе из цилиндра и соответствующим значением объемного расхода и температуры расплава при заданной темпе­ратуре стенок цилиндра. Стремятся определить расчетным путем такие характеристики двухмерного течения, как объемный расход поступательного течения, определяющий производительность про­цесса; значения градиентов давлении в поступательном и циркуля­ционном течениях, определяющих давлен ие и осевое усилие в зоне дозирования, и др.

(3.9)

Объемный расход О поступател ьного потока для случая плоского моделирующего течения определяется следующим выражением:

О — HwFd Jvz Cn) = *i = ЧС(П|),

П N +2

Где Fd — коэффициент формы противотока, равный

Х] — безразмерная координата (ri = y’7i); Uz =7tDNcos<p;

(3 8)

W = — zr/f)sm<p/7; t — 7i/)tgcp

(3.10)

IIpc >изводительность экструзии псевдопластичной жидкости оп­ределяется как

^ 2а FdN , . П + 2

Здесь

А = — {е/г^тфсовф,

А параметр выбирается по специальным номограммам в зави­симости от безразмерного градиента давления В, равного

В_ dP/dx (dP/dxY‘

Где (DP/Dx) * — норми рующии градиент да влений, при котором HQ = 0.

Для определения объемной производительности цилиндрическо­го червяка в политропическом режиме предложено уравнение сле­Дующего вида:

Где к{1) —значение коэффициента политропичности, зависящее от места расположения сечения на оси червяка; R = ebx Jj (— началь­ный коэффициент консистенции.

Для расчета производительности зоны питания (загрузки) обозна­чим независимую обт. емную производительность этой зоны симво­лом О *, независимую объемную производительность зоны плавле­ния — О’, независимую производительность зоны дозирования — О

Такие значения объемной производительности характеризовали бы каждою из зон, если бы процессы, протекающие в них, не зависе­ли друг от друга. Изделия хорошего качества получаются, когда со­блюдается условие О" >0; > О* .Следовательно, зона дозирования

Определяет производительность процесса. Если Q* то режим

Работы экструдера станет нестабильным и качество изделии ухуд­шится

Объемная производительность зоны загрузки равна

„ , 2жг, sinGsincn 1 — I _ fcT smG

Q3 = vuwh = П NhD————- = 2aN———— {3.12)

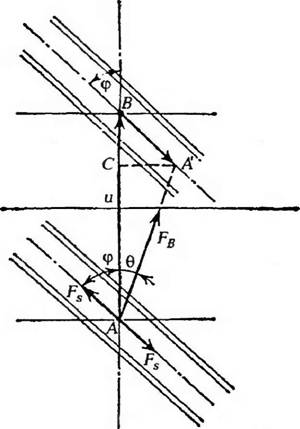
Где vn — скорость, с кот< >рой пробка перемещается по каналу, wи h — соответственно ширина и высота канала; N——• частота вращения чер вяка, D— диаметр канала, углы 0 и ф обозначены на рис. 3 24

Объемный расход зоны загрузки в 2 раза больше вынужденного потока (перемещение жидкости червяком с такими же размерами

Рис 3 24 Схема движения материала в зоне загрузки; корпус неподвижен, червяк движется

При отсутствии противодействия), рассчитанного для этой зоны Производительность зоны загрузки изменяется в зависимости ит соотношения коэффициентов грения пробки о стенки цилиндрами о поверхность канала t Максимальная производительность имеет место, когда пробка материала движется но каналу с такой же скоро­стью, с какой червяк перемешается относительно корпус а, т. E.Fb«/. Давление в зоне питания практически рассчитывают по формуле

В, — АЛ л

4+1 D (3 13)

А2к+В2

Где конический сердечник заменен ступенчато цилиндрическим, а /* — порядковый номер ступени, А., А, В. и В — параме гры. завися­щие от геометрии червяка, режима работы экструдера и реологи­ческих свойств перерабатываемого материала.

Как упоминалось выше, пробка материала движется с проскаль­зыванием относительно поверхности. За счет трения на поверхнос­ти контакта выделяется тепло. Около 95% работы трения расходует­ся на поверхности контакта пробки с внутренней поверхностью кор­пуса Количество тепа, выделяющегося в ндини! iy времени на участ­ке поверхности корпуса диной Dz, равно

DWb = vnPibwdz = nND ~^—fbwPdz. (3 14)

Так как dVTЈ пр< >порциопально локальному давлению Р, то оно дол­жно экспоненциально возрастать по длине канала Однако это имеет место только до тех пор пока поверхностные слои пробки не на гре­лись до температуры плавления. В области образования слоя рас­плава оканчивается зона питания к начинается переходная зона. Употненио пробки начинается практически, когда толщина слоя расплава становится в 4 — 5 раз больше радиалъног о зазора.

С этого начинается продвижение материала по зоне плавления. Длину участка червяка, на протяжении которого толщина слоя рас­плава достигает значений, необходимых для проявления механизма уплотнения пробки рассчитывают по уравнению

W + z{

Где oR—радиаьный зазор: р$—плотность материала пробки со = fiwp^; Va — скорость перемещения пробки, Zf— расстояние от конца зоны загрузки до сечения, в котором температура поверхности пробки достигла температуры плаьления.

Зона плавления следует за переходной зоной Как упоминалось выше, плавление материала начинается на поверхности его контак­та с горячей стенкой корпуса. Образующаяся на стенке корпуса плен­ка расплава постепенно по мере продвижения расплава утолщается и, когда ее толщина превысит значение радиального зазора между червяком и корпусом, передняя кромка стенки винтового канала нач­нет соскребать слой расплава. Этот слой собирается у толкающей стенки вин гового канала Ширина пробки материа ла по мере ее про­движения по каналу все время уменьшается вследствие плавления

При расчетах параметров зоны плавления исходят из того, что поля скоростей и температур в каждом сечении канала не зависят от времени и что область расплава отделяется от области гранул четкой границей (ка к будто полимер характеризуется четко проявляющей­ся температур* >й плавления) Пробка гранул принимается гомоген­ной и непрерывной. Считается, что поперечное сечение областей расплава и пробки является прямоугольным Теплопередача осуще­ствляется от внутренней поверхности корпуса 1 (рис. 3 2э) через дви­жущуюся пленку расплава 2 к твердой пробке 4. Кроме того, допол — н ительные порции тепла поступают за счет внутреннего трения

Обычно принимают толщину слоя гранул бесконечно большой, что в принципе д< шусти мо, так как коэффициент теплопроводности I ранул очень мал и, как видно из рис. 3.25, температура гранул быст­ро уменьшается и становится практически постоянной на всем рас — стоянии пробки по толщине. Скорость движения поверхности кор­пуса относительно червяка составляет 10 — 100 см/с.

0

Рис 3,25. Теоретическое распределение температур в расплаве и пробке 1 — внутренняя поверхность корпуса.

2 — расплав; 3 — поверхность раздела фаз; 4 — пробка

Течение тонкого слоя расплава рассматривается как вынужден­ное течение между двумя бесконечными параллельными плоскостя­ми* внут ренней поверхностью развертки корпуса, которая движется со скоростью v и имеет температуру Th, и поверхностью раздела фаз, температура которой 7 равна температуре плавления материала. Поверхность раздела фаз движется вдоль канала со скоростью v. Учитывая, что количество тепла q^, расходуемого на плавление ма­териала на < д инице поверхности раздела I равно разности между ко­личеством тепла / , подводимого к поверхности раздела, и количе­ством тепла (/_ , отводимого от нее и твердой пробки, получают

V^Lffa — Т9) + — ^-Ь—~РМТ9 ~ТОК (316)

Где v— проекция нектора скорости движения пробки, X — теплота плавления материала; к.— коэффициент теплопроводности распла­ва при средних значениях температуры и давления; ра— эффею ив — ная вязкость при градиенте скорости Avb/6 — разность скорос­тей движения корпуса цилиндра и пробки; 6 —толщина слоя распла­ва) ; с — теплоемкость материа ла.

Если ширину пробки обозначитьX. то скорость плавления на еди­нице длины канала ау можно рассчитать из уравнен ия материально­го баланса

W = vsyXPs =0,5V5A6 Р> (3.17)

Где vgx — проекция вектора скорости движения пробки.

Толщину слоя расплава р можно выразить как функцию ширины npof. ки Хи физиче< :ких характеристик полимера и режима экструзии:

(3.18)

8 =

05

Выше мы упоминали, что в рассматриваемом случае производи­тельность экстру дера определяется производительностью зоны до­зирования, равной

MN

О =——— (3.19)

R—1 ‘

Где М = /ф0ЬЯ/(рср); Е = — i"e)(l + 3sin’ф)/Л-ze/5 — ctgv;

К= + 2ас; с = 0,5(Гь +TS -270).

Таким образом, на примере экструзии пленок мы видим, что в насто­ящее время созданы предпосылки для научно обоснованного выбора оптимальных параметров технологического процесса Математичес­кое моделирование процесса находится на подии моделирования рео — логическ их процессов, протекающих в канале червяка экструдера и в его формующем приспособлении. Полученные с известной степенью приближения уравнения позволяют установить ко. личественные соот­ношения между параметрами конструкции червяка и головки, свой­ствами расплава и некоторыми па[ >амотрами процесса (произв< бдитель­ностью, давлением и темпера турой в зонах экструдера).

Задачи, стоящие перед технол< >гом, обы чно формулируются шире. I Томимо производительности экструдера переработч ик должен обес-

Печивать оптимальное сочетание эксплуатационных характеристик получаемых пленок. Это, как было показано на примере производ­ства рукавной пленки, не исчерпывается варьированием реологи­ческих и теплофизических характеристик процесса, протекающего в экструдере Режимы охлаждения, раздуьа, складывания рукава и другие ф жгоры оказываются иногда решав >щими при производстве пленок этим методом.

Приведенный пример моделирования процессов экструзии ру­кавных пленок является базой для создания системы автоматическо­го управления такими процессами.

Технология и оборудование для производства рукавных пленок относительно просты и получили широкое распространение в изго­товлении пленок ПЭ, П11 ПВХ, ПВДХ, ПК, АЦ и др.

К недостаткам этого способа относятся:

•низкая эффективность воздушного охлаждения;

• пониженная производительность и прозрачность (особенно ПП) пленок,

• неравномерная толшина пленок;

•склонность к складкообразованию пленок.

Производство тары из полимерных пленок и листов

Особенности механических свойсть полимеров в высокоэластическом состоянии

Интервал температур, в котором можно наблюдать высокоэлас­тические свойства полимеров, равен разности температур (Т — Т) Для сетчатых полимеров верхним пределом эластических свойств является температура начала термического разложения Т, так как из-за межцепных химических связей полимер течь не может и при высоких температурах начинает разлагаться, деструктироваться, не переходя в текучее состояние Эластические свойства целесообразно рассмотреть на […]

Производство мягкой потребительской тары на фасовочно-упаковочных автоматах термоформовочного типа

Термоформовочные автоматы позволяют упаковывать любые виды продукции с использованием всех возможных методов ее по­дачи в отформованную часть тары. 11ижняятермоформованная часть из однослойного или многослойного полимерного материала являет­ся жесткой или полужесткой. Верхняя крышка отличается гибкос­тью, минимальной жесткостью. Она выполнена, как правило, из мно­гослойного материала, поэтому обладает хорошими барьерными свойствами, способностью к сварке ил и склеиванию, пригодна […]

Контакт но-тепловая сварка

Контактно-тепловую сварку нагретым ин< трументом осуществ­ляют с односторонним или л, вусторонним нагревом (рис. 4.41). Рис. 4.41. Схема контактно-тепловой сварки с од] юсторонним (а) и двусторонним (6) нагревом: 1 — нагретый инструмент; 2 — прокладки; 3 — свариваемые материалы; 4—холодный инструмент, мгн — температура нагретого инструмента; t2 — температура внешней поверхности изделия; Т —температура свариваемых поверхностей; […]